Implicit derivative of (x²y²)³=5x²y² Implicit derivative of (x²y²)³=5x²y² If you're seeing this message, it means we're having trouble loading external resources on our website If you're behind a web filter, please make sure that the domains *kastaticorg and *kasandboxorg are unblockedFind and interpret the partial derivatives of f (x,y)=3x2y4 Find the derivative of f (ln (x)) given f (x)=x^22x Find all the horizontal asymptotes of (52^x)/ (12^x) Detailed Instructions for Solving Linear Differential Equations using Integrating Factors Convert the equation ydxxdy=0 toInteractive graphs/plots help visualize and better understand the functions

Implicit Differentiation Advanced Example Video Khan Academy
Partial derivative of 1/(x^2+y^2+z^2)
Partial derivative of 1/(x^2+y^2+z^2)-The derivative is an important tool in calculus that represents an infinitesimal change in a function with respect to one of its variables Given a function , there are many ways to denote the derivative of with respect toIn math, a derivative is a way to show the rate of change or the amount that a function is changing at any given point If you have a function f(x), there are several ways to mark the derivative of f when it comes to xThe common way that this is done is by df / dx and f'(x)If a derivative is taken n times, then the notation d n f / d x n or f n (x) is used



Derivatives Of Inverse Trigonometric Functions
Derivative calculator This calculator evaluates derivatives using analytical differentiation It will also find local minimum and maximum, of the given function The calculator will try to simplify result as much as possible Derivative Calculator Find Local Extrema (explained) The derivative of x2 is 2x Thus, using the chain rule, the derivative of sin x2 is cos x2 times 2x or just 2x cos x2 Step 1 Differentiate with the Chain Rule The derivative of ln x is 1/x, so the derivative of ln x2 is 1/x2 times the derivative of x2 Step 2 SimplifyThen, the derivativeDifferentiate both sides of the equation with respect to x, assuming that y is a differentiable function of x and using the chain rule The derivative of zero (in the right side) will also be equal to zero Note If the right side is different from zero, that is the implicit equation has the form f
The derivative of the function `y = log(x 1/x)` with respect to x, `dy/dx` has to be determined It is assumed that log in the problem refers to natural logarithm Use the chain rule hereDifferentiation is the action of computing a derivative The derivative of a function y = f(x) of a variable x is a measure of the rate at which the value y of the function changes with respect to the change of the variable xIt is called the derivative of f with respect to xIf x and y are real numbers, and if the graph of f is plotted against x, derivative is the slope of this graph at eachDifferentiate (x^2 y)/(y^2 x) wrt x;
Thank you for your help derivativeofafunction;//googl/JQ8NysPartial Derivative of f(x, y) = xy/(x^2 y^2) with Quotient RuleAsked in CALCULUS by linda Scholar Share this question




Derivative 2nd Order Learn Mathematics Online




Y X 1 X 2 X 3 X Find Its 1st Ordered Derivative Brainly In
Example using implicit differentiation to get the second derivative of y wrt x Uses substitution to get final expressionThis video screencast was createdThe Derivative Calculator supports computing first, second, , fifth derivatives as well as differentiating functions with many variables (partial derivatives), implicit differentiation and calculating roots/zeros You can also check your answers!Partial derivative of y/ (1x^2y^2) \square!



What Is The Derivative Of Y X 1 2 Quora




Find The Derivative 1 Y X 3 3 X 2 Pi 2 2 Y Chegg Com
FREE EXPERT ANSWERS Derivative of Euclidean norm (L2 norm) All about it on wwwmathematicsmastercomCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyThis preview shows page 169 174 out of 2 pages Find the derivative of the function f ( x ) = 1 x 2 6 Solution 615 By the Reciprocal Rule, we have f ( x ) = d dx ( x 2 6) ( x 2 6) 2 = 2 x ( x 2 6) 2 154 The derivative rules we have learned can be summarized as follow (1




Implicit Derivation Of Logarithmic Function Y Ln X 2 Y 2 Youtube




Find The N Th Derivative Of The Following 1 3x 5
Section 48 Derivatives of Inverse Functions Suppose we wanted to find the derivative of the inverse, but do not have an actual formula for the inverse function?Then we can use the following derivative formula for the inverse evaluated at \(a\text{}\) Theorem 480 DerivativeDerivative of Tangent Inverse In this tutorial we shall explore the derivative of inverse trigonometric functions and we shall prove the derivative of tangent inverse Let the function of the form be y = f ( x) = tan – 1 x By the definition of the inverse trigonometric function, y = tan – 1 x can be written as tanDerivative of 1/sqrt(1x^2) by x = x/(sqrt(1x)*sqrt(x1)*(x^21)) Show a step by step solution;



Curve Sketching
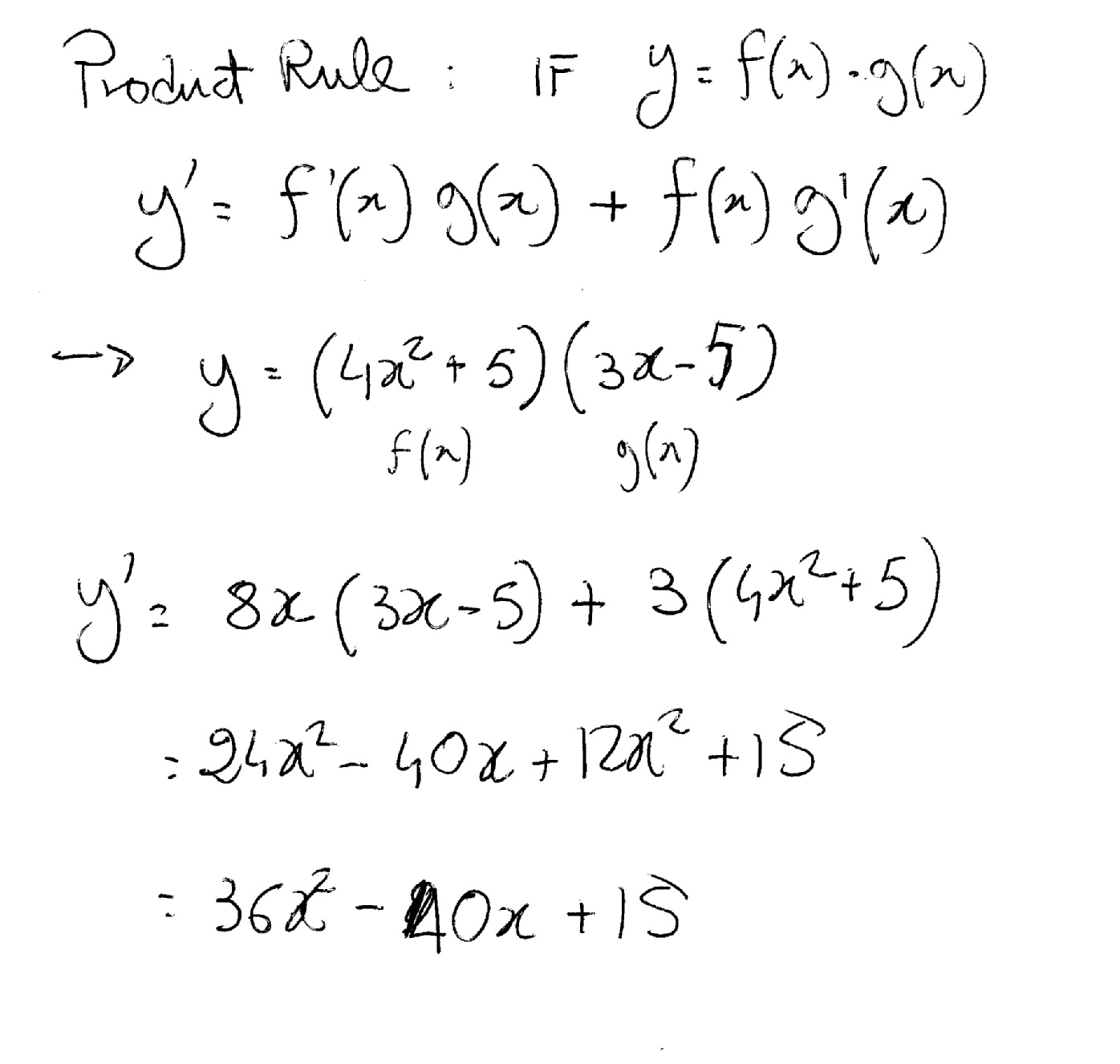



How Do You Use The Product Rule To Find The Derivative Y 4x 2 5 3x 5 Socratic
Find the derivative of x^2 cotx 1/x^2 0 votes Should I use the product rule first and then the subtraction rule?Question Find All The First And Second Partial Derivatives Of F(x, Y) = X^2 Y^2 Find All The First And Second Partial Derivatives Of F(x, Y) = Squareroot 1 X^2 Y^2 Find All The First And Second Partial Derivatives Of F(x, Y) = 1/x^2 Y^2 1Derivatives are fun and easy (not to mention handy in understanding the universe) You asked for the derivative of x^1/2 Simply pull the exponent to the units place and subtract 1 from the exponent So Step 1 Exponent to units place1/2x^1/2 Step 2 Subtract 1 from the exponent 1/2–1= 1/2 Put it back together1/2x^1/2 Hope this helps Jami



Solved Find The Derivatives 1 Y X 1 X 5 2 Y Log X 2 3 Y 5x Course Hero



Implicit Differentiation
This problem might have been given in preparation for introducing "e" The derivative of 2 x is lim h → 0 2 x y − 2 x h = lim h → 0 2 x 2 h − 2 x h = lim h → 0 ( 2 h − 1 h) 2 x / i t e x t e x = ( lim h → 0 2 h − 1 h) 2 x That is, of course, a constant times 2 x Similarly, the derivative of 3 x is = ( lim h → 0 3Answer to Find the partial derivative of the function u=ln (x^2y^2z^2) By signing up, you'll get thousands of stepbystep solutions to yourY1 = f1 (x1,x2) y2 = f2 (x1,x2) ∗Each equation has two firstorder partial derivatives, so there are 2x2=4 firstorder partial derivatives — Jacobian matrix array of 2x2 firstorder partial derivatives, ordered as follows J= ∂y1 ∂x1 ∂y1 ∂x2 ∂y2 ∂x1 ∂y2 ∂x2 — Jacobian determinant determinant of Jacobian matrix




Implicit Differentiation Advanced Example Video Khan Academy




Solved Verify That The Function U 1 Sqrt X 2
Find the Derivative f(y)=y/(x^2y^2) Differentiate using the Quotient Rule which states that is where and Differentiate Tap for more steps Differentiate using the Power Rule which states that is where Multiply by By the Sum Rule, the derivative of with respect to is Calculate the partial derivatives of $\sin(x^2y^2) $ with the limit definition of the partial derivative Ask Question Asked 1 year, 3 months ago Active 1 year, 3 months ago Viewed 277 times 0 $\begingroup$ Here's what I have so far $$\frac{\partial fPlease Subscribe here, thank you!!!
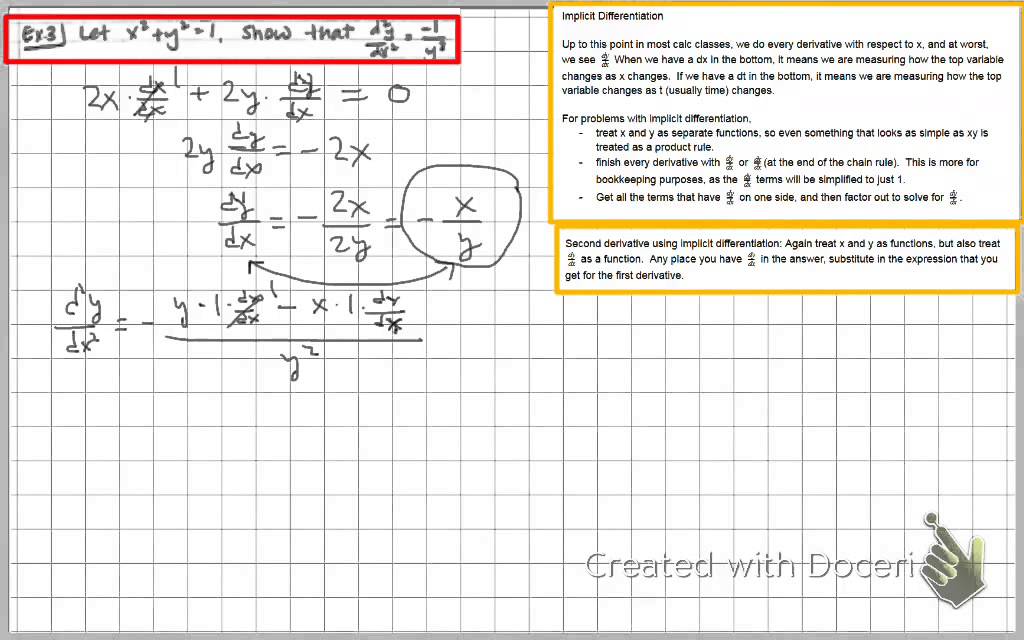



Calculus Find Second Derivative Of X 2 Y 2 1 Youtube




Ex 5 7 1 Find Second Order Derivatives Of X2 3x 2
Draw graph Edit expression Direct link to this page Value at x= Derivative Calculator computes derivatives of a function with respect to given variable using analytical differentiation and displays a stepbystep solution It allows to draw graphsClick here👆to get an answer to your question ️ The derivative of y = (1 x)(2 x)(n x) at x = 1 is equal toDerivative is the important tool in calculus to find an infinitesimal rate of change of a function with respect to its one of the independent variable The process of calculating a derivative is called differentiation Follow the rules mentioned in the above derivative calculator and understand the concept for deriving the given function to




Find The Derivative Of Y 1 X 2 X N X At X 1 Brainly In




Copyright C Cengage Learning All Rights Reserved Partial Derivatives Ppt Download
Online Question and Answer in Differential Calculus (Limits and Derivatives) Series Following is the list of multiple choice questions in this brand new series MCQ in Differential Calculus (Limits and Derivatives) PART 1 MCQ from Number 1 – 50 Answer key PART 1 PART 2 MCQ from Number 51 – 100 Answer key PART 2Derivatives and Integrals of the Hyperbolic Functions d y d x = 1 cosh y = 1 1 sinh 2 y = 1 1 x 2 d y d x = 1 cosh y = 1 1 sinh 2 y = 1 1 x 2 We can derive differentiation formulas for the other inverse hyperbolic functions in a similar fashion These differentiation formulas are summarized in the following table Figure 684 There's a factor of 2 missing in all your second derivatives The result is exactly as you'd expect The variable you're differentiating with respect to, matters If it's x, then y is treated as a constant, and vice versa So if the "active" variable is leading in the numerator in one derivative, the same should apply in the other



Second Derivative Concavity
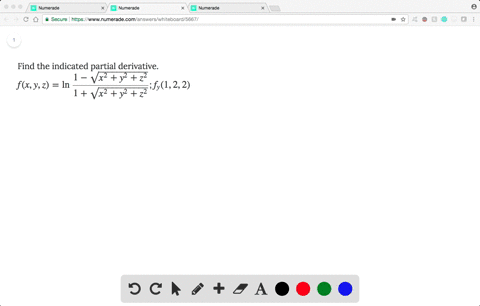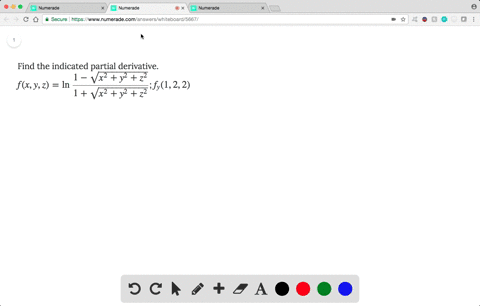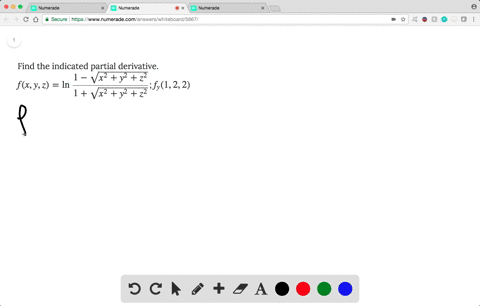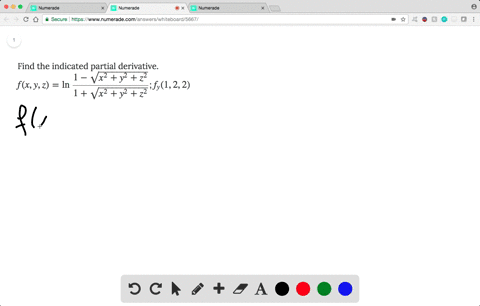



Solved Find The Indicated Partial Derivative F X
If y = xsqrt(1 x^2) then y^2 = x^2(1 x^2) = x^2 x^4 Now differentiate implicitly 2ydy = (2x 4x^3)dx, therefore, cancel 2s and x and make dy/dx the subject of the formula ydy = (x 2x^3)dx = x(1 2x^2)dx => dy/dx = x(1 2x^2)/y => dy/Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!By treating x as a constant, we find f y =3x 2 3y 2 Second Partial Derivatives Observe carefully that the expression f xy implies that the function f is differentiated first with respect to x and then with respect to y, which is a natural inference since f xy is really (f x) y For the same reasons, in the case of the expression,




What Is The Derivative Of Sqrt X 2 1 X 2 1 Socratic




Ex 13 2 9 Find Derivative Of I 2x 3 4 Ii 5x 3 3x 1 X 1
Using Implicit Differentiation and the Product Rule Assuming that y is defined implicitly by the equation x3siny y = 4x 3, find dy dx Solution d dx(x3siny y) = d dx(4x 3) Step 1 Differentiate both sides of the equation d dx(x3siny) d dx(y) =Let's look more closely at how d dx (y 2) becomes 2y dy dx The Chain Rule says du dx = du dy dy dx Substitute in u = y 2 d dx (y 2) = d dy (y 2) dy dx And then d dx (y 2) = 2y dy dx Basically, all we did was differentiate with respect to y and multiply by dy dxImplicit\derivative\\frac {dy} {dx},\ (xy)^2=xy1 \frac {\partial} {\partial y\partial x} (\sin (x^2y^2)) \frac {\partial } {\partial x} (\sin (x^2y^2)) derivativecalculator \frac {d} {dx}\left (\frac {1} {x^ {2}}\right) en Sign In Sign in with Office365 Sign in with Facebook




Find All The Second Order Partial Derivatives Of The Chegg Com
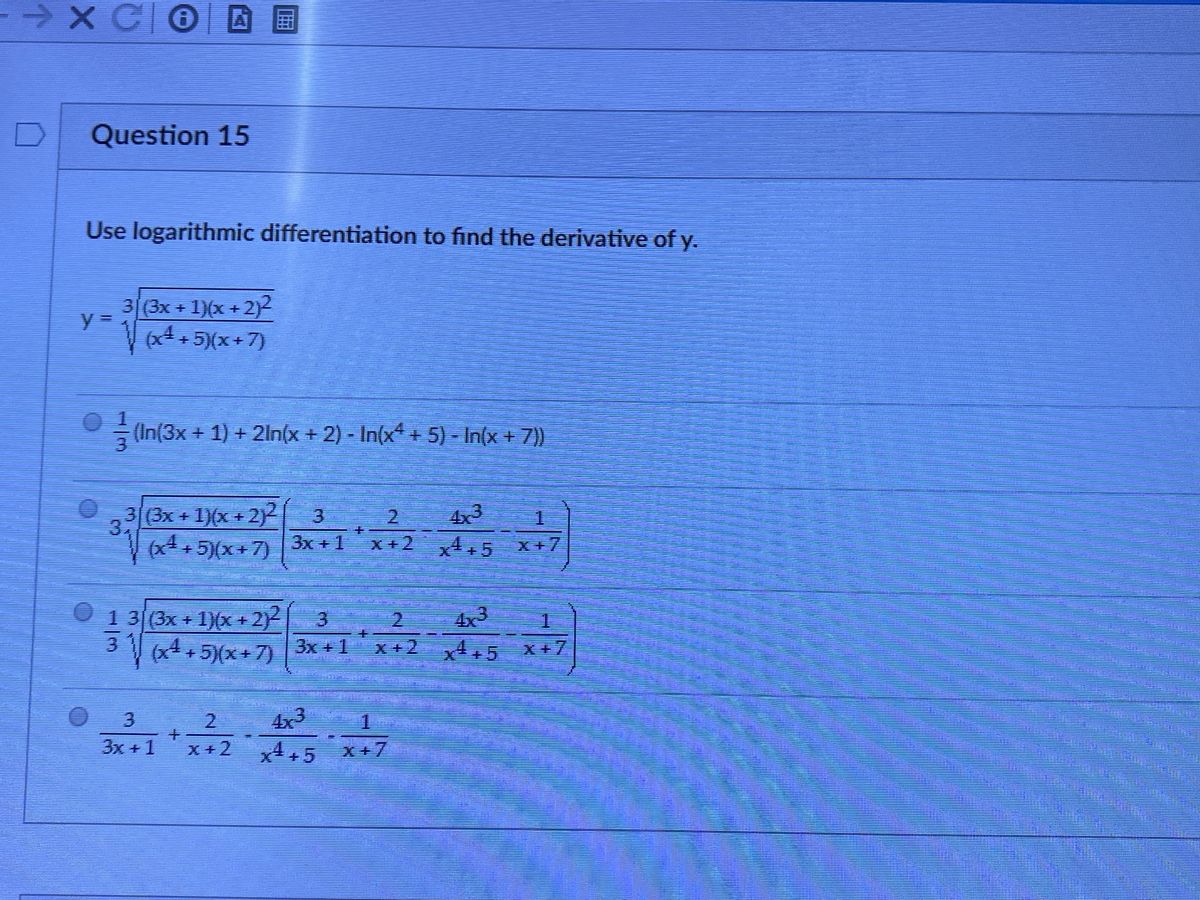



Answered Use Logarithmic Differentiation To Find Bartleby
Draw graph Edit expression Direct link to this page Value at x= Derivative Calculator computes derivatives of a function with respect to given variable using analytical differentiation and displays a stepbystep solution It allows to draw graphs ofD x d y = 1 − x 2 y 2, Given Here, d x d y represents the derivative of y with respect to x I will solve for x and y, treating y as a function of x (essentially y = f (x)) ∫ d x d y d x = ∫ 1 − x 2 y 2Derivative of x/(x^2y^2) by x = (y^2x^2)/(y^42*x^2*y^2x^4) Show a step by step solution;



5 Derivative Of The Logarithmic Function




Answered 7 Find The Second Partial Derivatives Bartleby
Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange differentiating #x^2y^2=1#, we get #2x2y(dy)/(dx)=0# ie #(dy)/(dx)=x/y# and differentiating it further #22(dy)/(dx)(dy)/(dx)y*(d^2y)/(dx^2)}=0# or #22(dy)/(dx)^22y(d^2y)/(dx^2)=0# or #22x^2/y^22y(d^2y)/(dx^2)=0# or #2y(d^2y)/(dx^2)=22x^2/y^2# or #(d^2y)/(dx^2)=2/(2y)2x^2/y^2*1/(2y)# = #1/yx^2/y^3#What is the directional derivative of the function f(x,y,z)= xyz / 1 (x^2)(y^2)(z^2) at the point P(1,1,1) in the direction s=i4kj




Find The Partial Derivative Of F X Y E X2 Y2 With Chegg Com




Derivative Of F X X 2 1 X 3 1 Using The Product Rule Youtube
Popular Problems Calculus Find the Derivative d/dx (x^2y^2)^ (1/2) (x2 y2)1 2 ( x 2 y 2) 1 2 Differentiate using the chain rule, which states that d dx f (g(x)) d d x f ( g ( x)) is f '(g(x))g'(x) f ′ ( g ( x)) g ′ ( x) where f (x) = x1 2 f ( x) = x 1 2 and g(x) = x2 y2 g ( x) = x 2 y 2It is the same deal with sin and arcsin, which is conventionally written as sin^1 x Arcsin is the inverse of sin, such that arcsin (sin (x)) = x, or sin (arcsin (x))=x Like the square/square root example, if you have y=sin (x), which is y in terms of x, but you want to take that expression and find x in terms of y, then given y=sin (x) take tan1 (x 2 y 2) = α ⇒ x 2 y 2 = tan α Differentiating wrt x, we get 2x 2y dy/dx = 0 ⇒ dy/dx = x/y




Math 277 Example Gradient And Directional Derivative




1 6 Topics Using Basic Differentiation Rules Solutions
Answer and Explanation 1 a Using implicit differentiation to find the first derivative, we have 2x3 y2 = 1−4y 6x2 2ydy dx = −4dy dx 2 x 3 y 2 = 1 − 4 y 6 x 2 2 y d y d x = − 4 dSolution Steps { x }^ { 2 } { y }^ { 2 } 2y1 x 2 − y 2 2 y − 1 Rewrite as difference of two terms Rewrite as difference of two terms x^ {2}\left (y^ {2}2y1\right) x 2 − ( y 2 − 2 y 1) Rewrite the terms as squares Rewrite the terms as squares




Find The Derivatives W R T X Y 1 X 1 2x 1 3x 2 Youtube
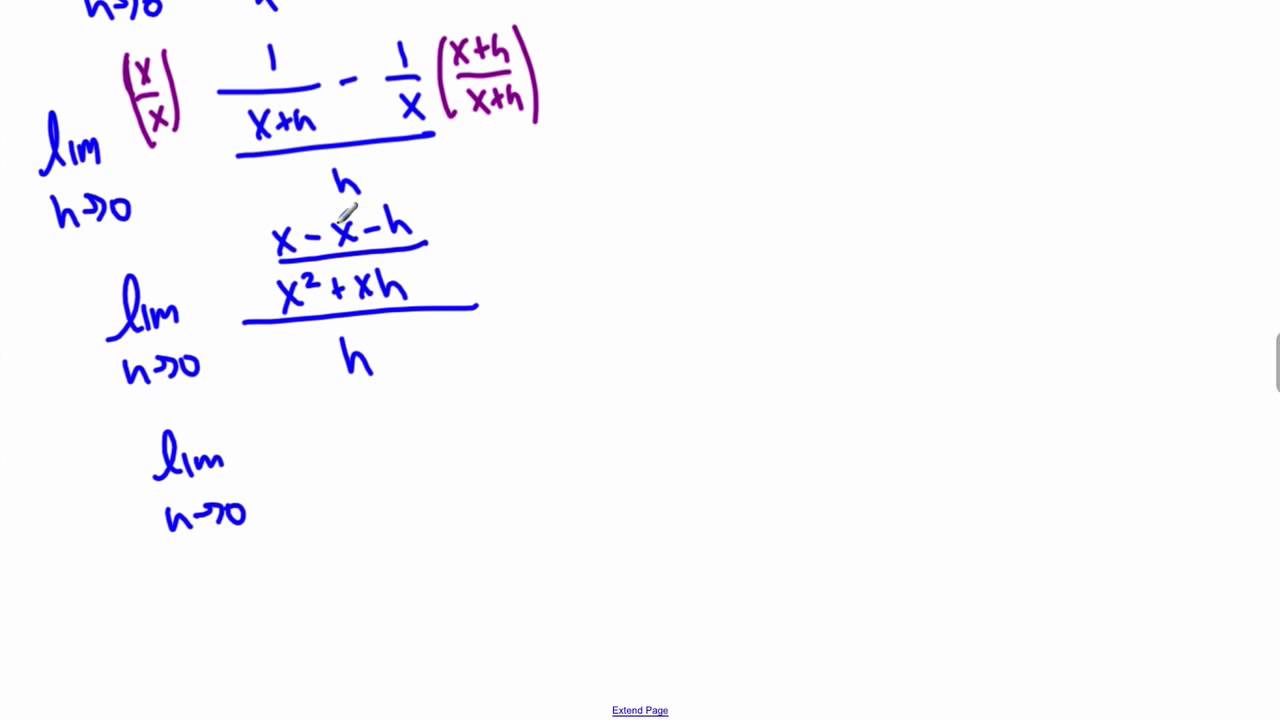



Definition Of Derivative Example Y 1 X Youtube




What Is The Implicit Derivative Of 1 Xy Xy Y 2 2y Homeworklib



Www Math Unipd It Umarconi Did Simmons Pdf




Derivative Of X 2 Y 2 Log Xy Youtube




Find The Derivative I F X X 2 Tan 1 X 1 Chegg Com




Find Dy Dx Y Sin 1 X2 1 X2 Mathematics Topperlearning Com 8s1l799
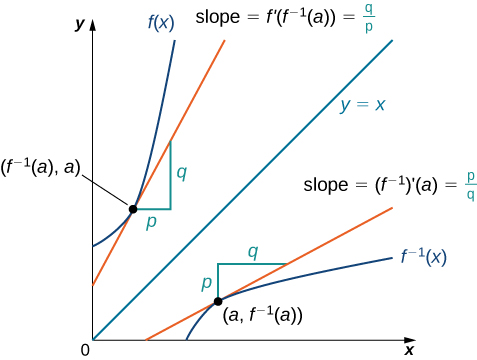



3 7 Derivatives Of Inverse Functions Mathematics Libretexts




Find The Derivative Of Y X X 2 1 With Respect To X Using Fir




Partial Derivative Math Help Forum




Solutions Manual For Calculus An Applied Approach Brief International




Basic Calculus Module Derivative Function Mathematics




Show That Z Ln X 2 Y 2 2 Tan 1 Y X Satisfies The Laplaces S Equation Mathematics Stack Exchange




Second Derivatives Implicit Equations Evaluate Derivative Video Khan Academy




If Y X X 2 Then The Derivative Of Y 2 With Respect To X 2 Is
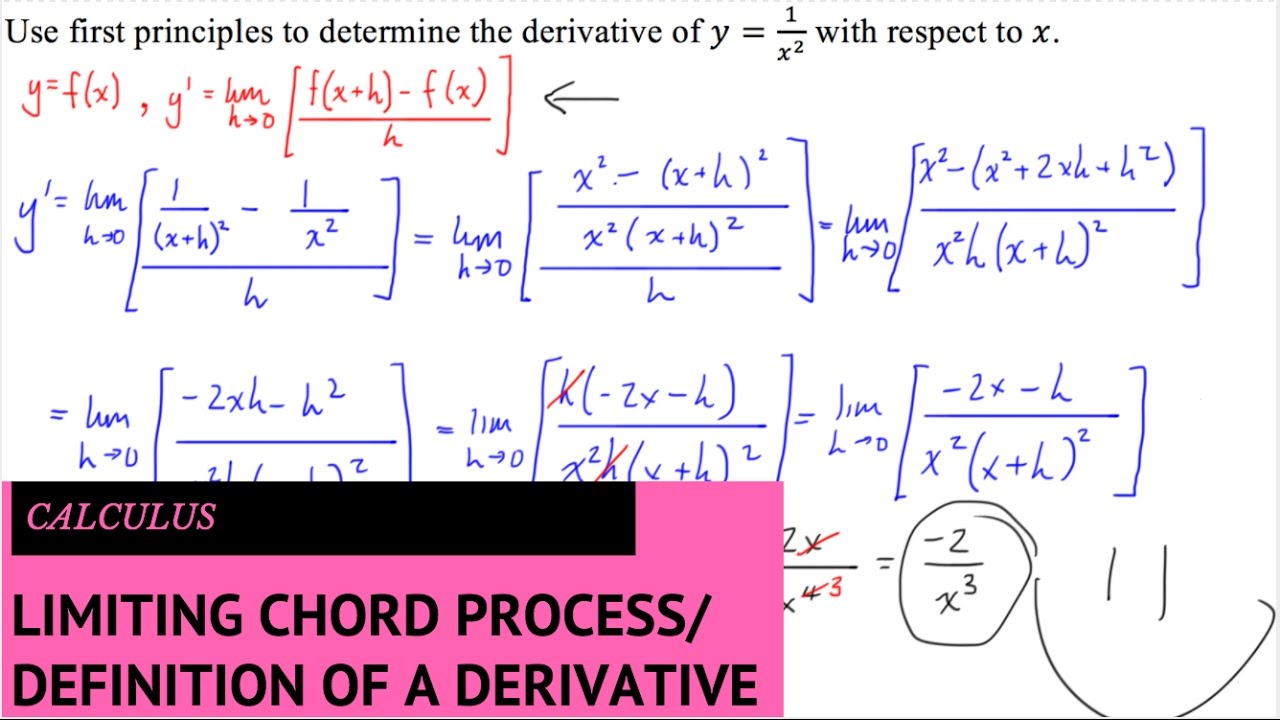



First Principles Derivative Limiting Chord Process Y 1 X 2 Youtube
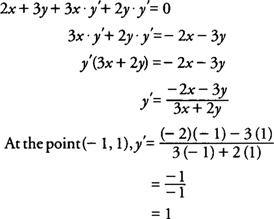



Implicit Differentiation




Implicit Differentiation




4 1 Implicit Differentiation



What Is The Differentiation Of 1 X 2 Quora



Derivatives Of Inverse Trigonometric Functions




Derivative Calculator Wolfram Alpha



4 2 Implicit Differentiation



Www Ucl Ac Uk Ucahjva Multi4 Pdf
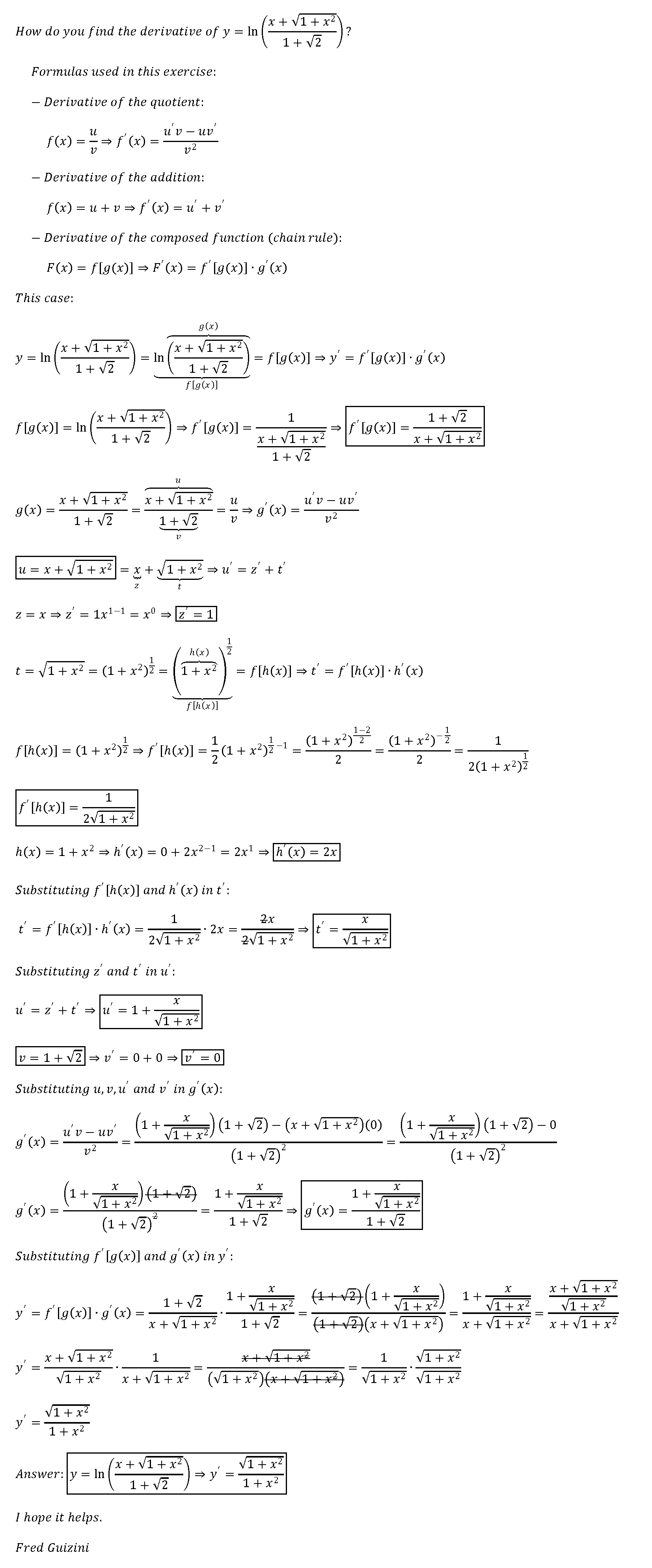



How Do You Find The Derivative Of Y Ln X Sqrt 1 X 2 1 Sqrt2 Socratic




Derivative Rules




You Can Do It 2 5 Implicit Differentiation How Would You Find The Derivative In The Equation X 2 2y 3 4y 2 Where It Is Very Difficult To Express Ppt Download




Find The Derivatives W R T X Y 1 X 1 2x 1 3x 2




Partial Derivative Examples Math Insight




Implicit Differentiation




Partial Derivative Of F X Y Z With Respect To Z Mathematics Stack Exchange




Find The Derivative Of The Function Chegg Com



1




Find The Derivative Of Y Sqrt X 2 1



1



X 2 Y 2 1 Find Dy Dx By Implicit Differentiation Youtube



S3 Wp Wsu Edu Uploads Sites 2 19 08 Derivatives And System Of Eq Part 1 Ans Key Pdf
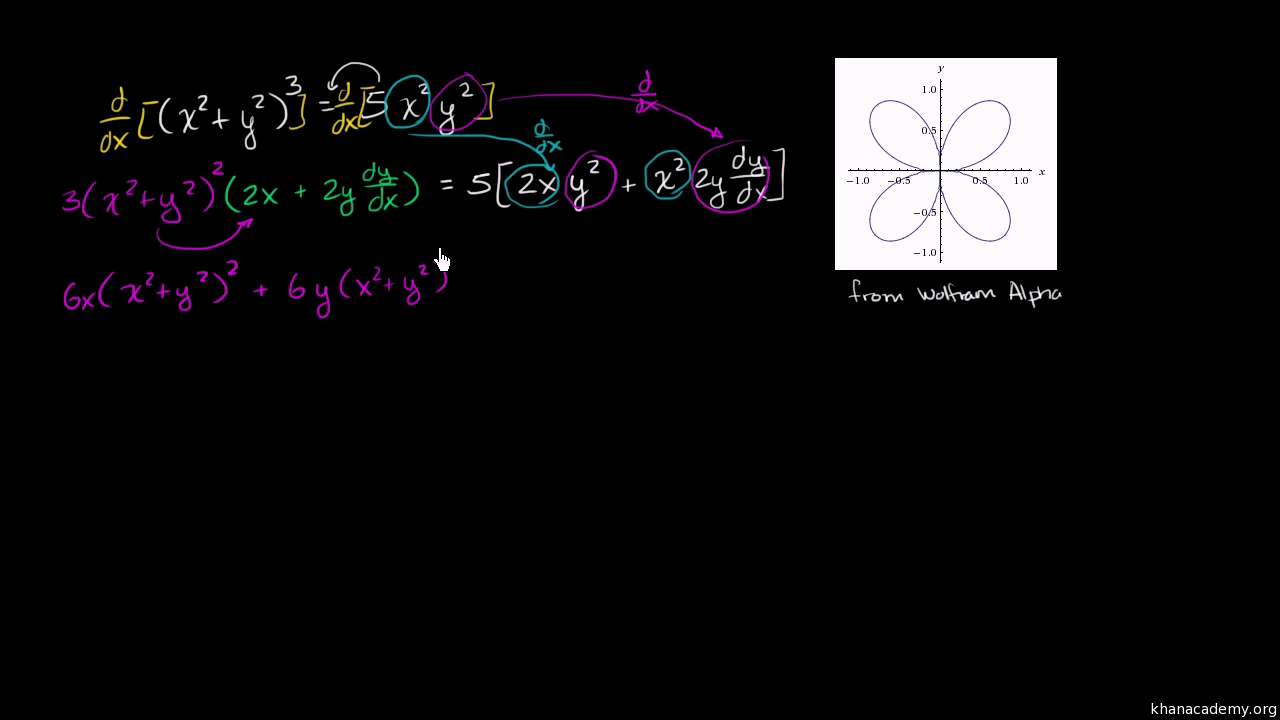



Implicit Differentiation Advanced Example Video Khan Academy




If Sqrt 1 X 2 Sqrt 1 Y 2 A X Y Show That Dy Dx Sqrt 1 Y 2 1 X 2 Mathematics And Statistics Shaalaa Com




1 Express The Limit As A Derivative And Evaluate 17 Lim 16 H 2 Lim 2 Calculate Y Tan X 1 Co Homeworklib




Partial Derivative Examples Math Insight



What Is Calculus



Derivative 1 2 1 2 Ln X 1 X 1 Arctanx Mathskey Com




Higher Derivatives Partial Differentiation




How To Find The Derivative Of Y X Sqrt X 2 1 Youtube
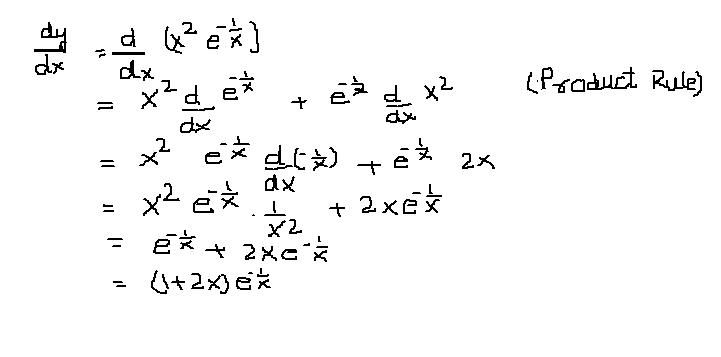



How Do You Find The Derivative Of Y X 2 E 1 X Socratic



Defining Calculus Study Guide




Answered Fin The Second Derivative Of The Bartleby



Q Tbn And9gcqnye10zfu7n1e5psc 7oyuuimkr8sjknkcqpbj1hdnr3gsgvai Usqp Cau




Partial Differentiation And Multiple Integrals Pdf Free Download
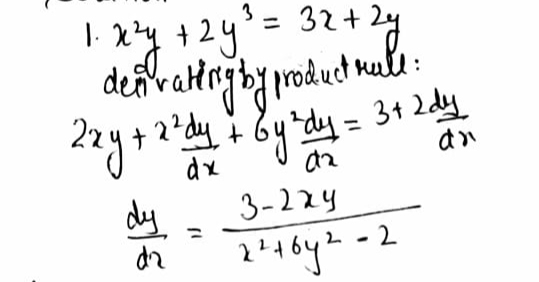



Learning Task 1 Determine The Derivative Of The F Gauthmath



Www3 Nd Edu Apilking Math Work Old exams Exam2f07solutions Pdf




Y X X 1 X 2 Calculate The Nth Derivative Of Y Brainly In




Implicit Differentiation



Class Take Your Seats



Q Tbn And9gcrrinrx Cj Exg3nxzq0njw Zkgdtymbulzjk0knpmztrmnoi4q Usqp Cau




5 Derivative Of The Logarithmic Function




Find The Indicated Partial Derivatives Math F W X Y Z Sqrt X Y Y Z X 3 Sin Sqrt W 2 Z 2 F X X F Y Y F W X Y Z Math Homework Help And Answers Slader



If Math Sqrt 1 X 2 Sqrt 1 Y 2 A X Y Math How Can I Prove Math Frac Mathrm D Y Mathrm D X Sqrt Frac 1 Y 2 1 X 2 Math Quora




Find The Derivative Of The Function Y 3 Sin 1 X 2 Chegg Com




You Can Do It 2 5 Implicit Differentiation How Would You Find The Derivative In The Equation X 2 2y 3 4y 2 Where It Is Very Difficult To Express Ppt Download



Business Calculus



Derivative Calculator With Steps
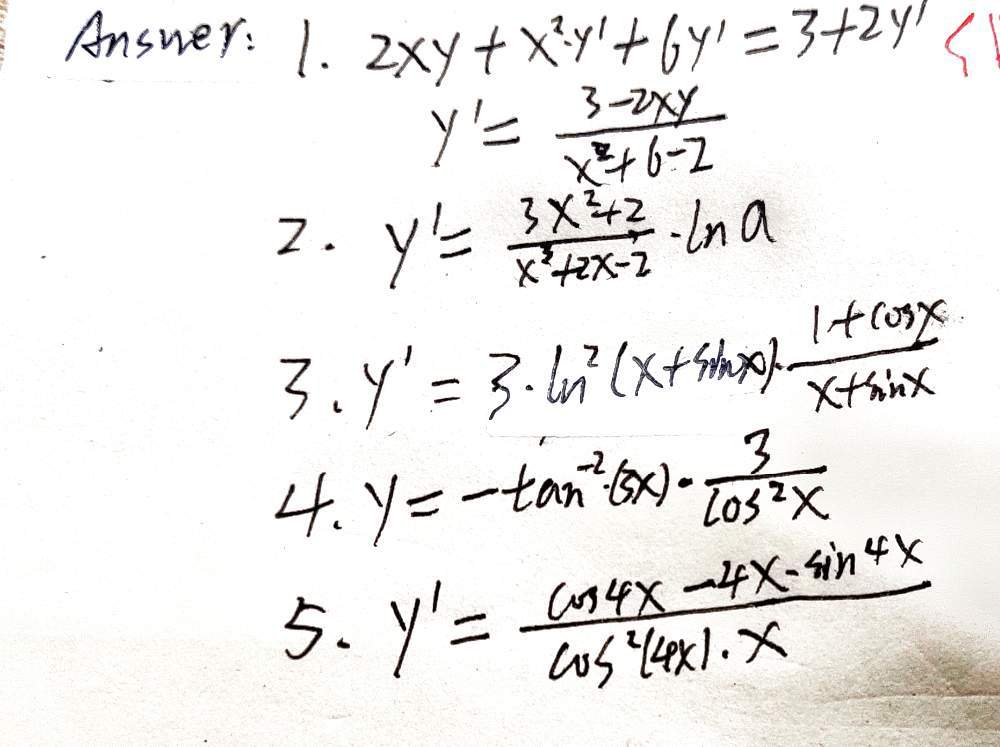



Learning Task 1 Determine The Derivative Of The F Gauthmath




Ex 5 7 12 If Y Cos 1 X Find D 2y Dx 2 In Terms Of Y Alone



What Is The Differentiation Of 1 X 2 Quora
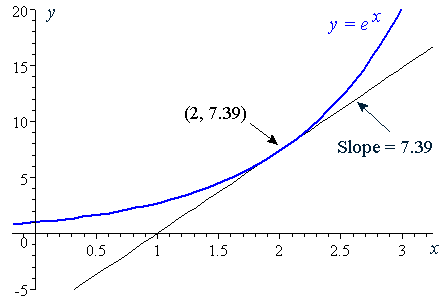



6 Derivative Of The Exponential Function




Find Dy Dx Y X 2 1 3 2x 1 Sqrt X 3 4x 1



Www Lcps Org Cms Lib Va Centricity Domain 2 5 notes filled out Pdf
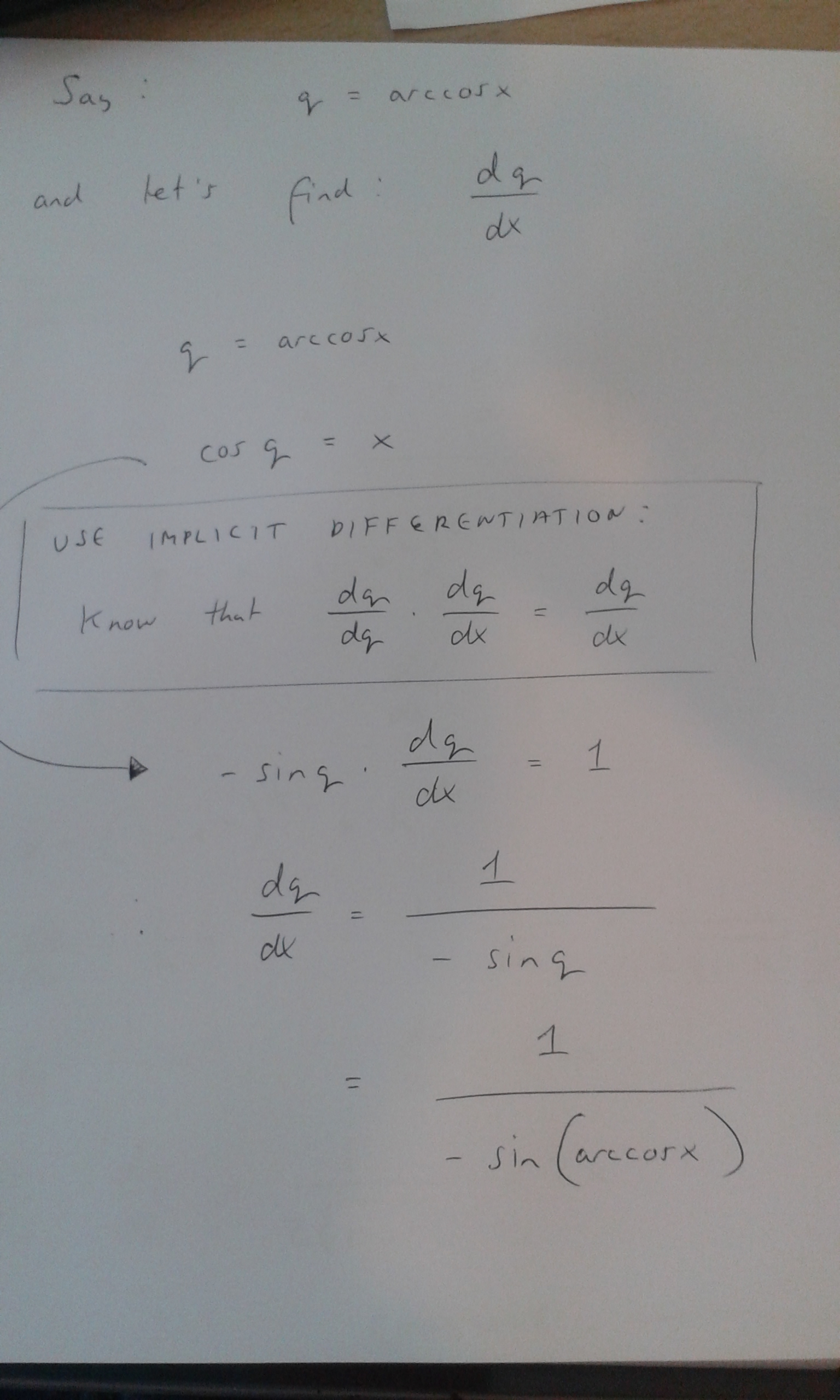



How Do You Differentiate Y Arccosx X Sqrt 1 X 2 Socratic




How Do You Find The Derivative Of Y 1 X 2 Cot 1 2x Socratic




How Can I Find The Nth Order Derivative Of 1 1 X X 2 Quora




Use Suitable Derivative Rules To Find Y If Y Chegg Com




What Is The Nth Derivative Of Arctan 2x 1 X 2 In Terms Of R And Theta Quora




Consider The Function F X Y Ln X 2 Y 2 3 Compute The Partial Derivatives Of The First And Second Order Mathematics Stack Exchange
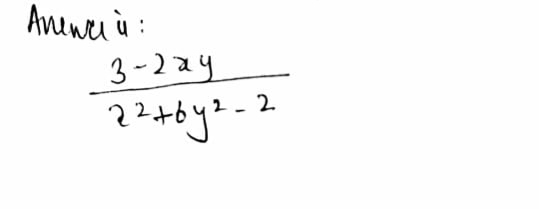



Learning Task 1 Determine The Derivative Of The F Gauthmath



0 件のコメント:
コメントを投稿