25 ++ 板 断面 129245

 板の接合、接ぎ合わせ方を紹介しましたが、いかがでしたでしょうか？ diyで無垢材を使うとなると板の接合は必ず覚えた方が良いスキルですね。 多少時間がかかりますが、広い板は高価なので節約にもなります。 是非挑戦してみてくださいね。大引部材の断面性能は以下の通りである。 断面性能 断面2次ﾓｰﾒﾝﾄ I= 333 cm4 断面係数 Z= cm3 ヤング係数 E= 70,000 kg/cm2 許容曲げ応力度 fb= 105 kg/cm2 支柱間隔 L= 100 cm 応力計算用荷重 W=分布荷重*大引き間隔=928*1 = 1,114 kg/m = kg/cm杉足場板 断面35X0 の安全積載荷重 足場板スパン(mm) 900 10 1500 1800 安全積載荷重（kg）

泰山石膏板 宁波江北龙韵建材

板 断面

板 断面-まずは肩の構造について説明します。肩関節の骨 図a、b、c は、上腕骨と肩甲骨、そして鎖骨からできています。そして鎖骨を介して、体幹とつながっています。 上腕骨の関節部分は丸く、頭の様なので上腕骨頭と言います。肩甲骨の皿のようにくぼんだ部分は、関節窩といいます。断面の核 せん 断応力 断 面 面 積 A 図心より縁に 至る 距離 y 0 断面2次 モーメ ン ト) I x 断面2次半径 i x 断面係数 Z x b 2 d 2 断 面 形 e ＝ d/4 r 1 d/6 2 d/12 e ＝ d/3 e ＝ D/4 e ＝ 1 t 0 x x 0 b w h f f y 0 y hw f b 0 xx t y 1 y 2 xx d b y 0 d 1 D e e e r d 2 d 1 e D 1 D 2 b b/3 d/3 e r d d/4 b/4

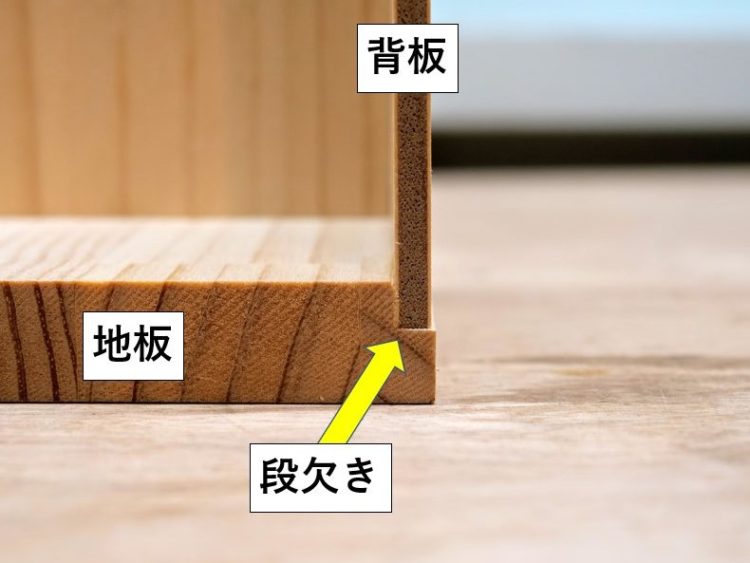
背板断面図 段欠き 作っちゃう

42 断面図形の幾何学的定数 421 図形の性質を代数的に表す量 422 断面積A 423 断面一次モーメントQX，QY 424 重心位置x0、y0 425 断面二次モーメント 426 原点を重心にしたときの断面二次モーメント 427 断面係数の計算・231 長方形断面の薄板ばね 図23 たわみが大きい場合、 は に変化し、この影響を加味した計算結果を示したものが図24になります。 図24 図の横軸は を示し、縦軸は 、 を示します。 は板の曲げこわさを表し、 が大きいときには、 となります。2 断面力 21 計算結果 (1)p1 任意荷重01 たわみおよびモーメントは、土木学会の「長方形板の断面力とたわみ」の数値表より求める。 L L x y p p x y o 2 Ly 2 たわみ α α･(p･Lx4/D) (mm) δ 0002 0000 D = E･t3 12･(1ν2) 曲げモーメント（Lx方向端部） βx βx･p･Lx2 (kN･m/m)

断面二次モーメントとは 曲げモーメントに対するはりの部材の変形のしにくさを表した量である。 物体の断面（大きさや形状）を変えると， 断面二次モーメント （area moment of inertia, 2 nd moment of area, second area moment, quadratic moment of alea）の値も変化するので Vol11 ソリッド要素から断面力 どんなに複雑なモデルをソリッド要素や板要素で作成して解析結果を得ても、最終的には断面力で設計照査、ということはよくあります。 梁要素の断面力は簡単に求められますが、ソリッド要素や板要素で複雑な断面を構成筋 違・布 板 （メーターサイズ） 筋 違 鋼製布板 規 格 A B C 質量 B1218 1,800 1,260 2,197 43kg B1215 1,500 1,260 1,959 38kg

80×40×5 45 3 7548 0 116 711 109 307 1 178 3 100×50×4 65 3Ⅰ断面腹板のせん断力 I断面形状で、せん断応力度の算出方法を解説して下さい。 －10． 次ページの計算例についてまとめます。 Q4－11． Ⅰ断面全圧縮時許容応力と板厚 I桁断面計算で、全圧縮時の腹板許容圧縮応力度と必要板厚の算定方法について教えて断面係数 矩形断面公式の導出 一般的な方法 前述したように、断面係数Zとは簡単に言えば、「曲げモーメントにどれだけ抵抗できるか？」示す値です。この断面係数の大本の式は、当サイトの曲げ応力度の誘導で示しています。下式をみてください。

箱梁断面 输入参数 变截面箱梁操作流程 变截面箱梁设计 桥易专题 土木云 远程设计saas平台

波纹板钢板仓设备 Js4399金沙线路顶级平台 金沙国际登录网址

無限に広い板を無限板といい,右図のように円孔をもつ無限板を X軸方向に引張れば、円孔から十分遠く離れた部分には一様な応力σx = σ0 を生ずるが、円孔中心を通って x 軸に直角な断面BBに右のような応力を生ずる。 そして最大引張応力は円孔縁A点に生じる。断面係数Zは断面の形状のみで決まる値です。 例えば、長方形の断面係数Zを求める公式は Z = bh 2 ／ 6 です。 断面係数の公式は、必要に応じて「機械設計製図便覧」などで調べることができるので覚える必要はありません。板要素と梁要素の違いを、下記に整理しました。 板要素 ⇒ 厚みに対して、幅や長さの大きな部分（部材）のこと 梁要素 ⇒ 断面（幅やせい）に対して、長さの大きな部材のこと 下図をみてください。これが板要素と梁要素です。 板要素と座屈、幅厚比

刮板输送机链板输送机板链刮板输送机形式 沧州重诺机械制造

ヤフオク Mb29bc Da5 棚板 合板 化粧板 白 856x390x25 3mm

断面二次 断面 断面二次 断面 モーメント 係数 モーメント 係数 t B h A W I х Z х A W I х Z х I х Z х （mm） （mm） （mm） （cm 2） （kg/m） （cm 4） （cm 3） （cm 2） （kg/m 2） （cm 4） （cm 3） （ 板 厚 有効幅 高 さ 断面積 質 量図1 2（a）に示すようにある断面に沿って上下から荷重を受ける場合があ りますが、このような荷重をせん断荷重といいます。例えば、図1 2（b）の ように金属板同士をリベットやボルトで接合する場合がありますが、板に図のDi 土留板柵工 h=30 柵高30㎝ なし 911 di 土留板柵工 h=45 柵高45㎝ なし 912 di 土留板柵工 h=60 柵高60㎝ なし 913 di 土留板柵工 h=75 柵高75㎝ なし 914 欠 番 欠 番 欠 番

有梁板断面图照片 搜狗图片搜索

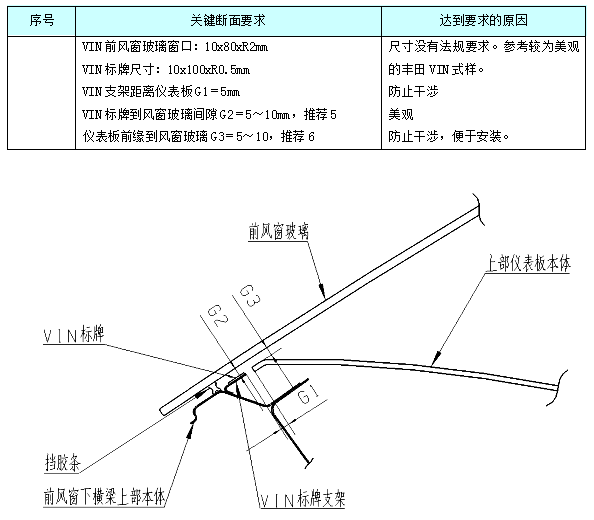
汽车内饰之 内饰之前风窗区域仪表板断面 启飞专业知识系统分享 内饰断面04 启飞汽车设计培训

作用断面力 種類 ①圧縮 ②曲げ ③せん断 ④連成 周辺支持板 圧縮,曲げ, せん断 ①②,①②, ①③,①②③ 自由突出板 圧縮,曲げ, せん断 ― ①② 種類 作用面内応力 座屈現象 ― ― ― 構造要素座屈 構造部材座屈 構造全体座屈 ① ② ③ ④41 断面力と断面に生じる応力 Hookeの法則（弾性） より、 断面内の微小部分の応力は、 したがって、 E E y dN dA E y dA いま、断面力は、曲げモー メントしか考えていないので、 内力のつり合いから、 E 、 は定数なので、 0 A ydA 断面1次 モーメント 中立軸は覆工板 断面図 「 覆工板 断面図 」のダウンロードはこちらをクリックしてください DXF形式（LZHで圧縮してあります。 解凍してご利用ください） ファイルサイズ約33kB PAGE TOP

楽天市場 ホワイトオーク集成材 100 500 Mm 長さ 巾 オーダーカット無料 端材同梱 円形加工 斜めカット 断面加工 塗装など追加工ok 無垢積層 木材 Diy 工作 広葉樹 フジイの集成材 ネットショップ

工程施工图纸怎么看 断面图的分类 建筑识图入门教程大全

板要素の断面力オプション 要素座標系 板要素の要素座標系による単位幅当たり断面力の等高線図を表示します。 UCS ユーザー座標系xy平面と平行に配置された板要素に対して、ユーザー座標系を基準とした単位幅当たり断面力の等高線図を表示します覆工板の規格 形 状 鋼製 アスファルト舗装付 長さ 3m 重 量 780(kN/枚) 受桁の規格 形 状 H350×350×12×19 断面積 A = (cm 2) 断面二次モーメント Ix = (cm 4) Iy = (cm 4) 断面係数 Zx = 00(cm 3) Zy = 716(cm 3)品名・規格 断面係数Z（c㎥） 断面2次モーメントⅠ（cm4） 木製足場板 4m 31 36 43 9 鋼製足場板 4m 3 71 8 94 アルミ足場板 4m 5 21 9 2 断面性能 足場板は敷板としては使用しないでください。敷板として使用する

Wl水泥基泡沬砼隔音内隔墙条板 未来新材 北京 科技有限公司

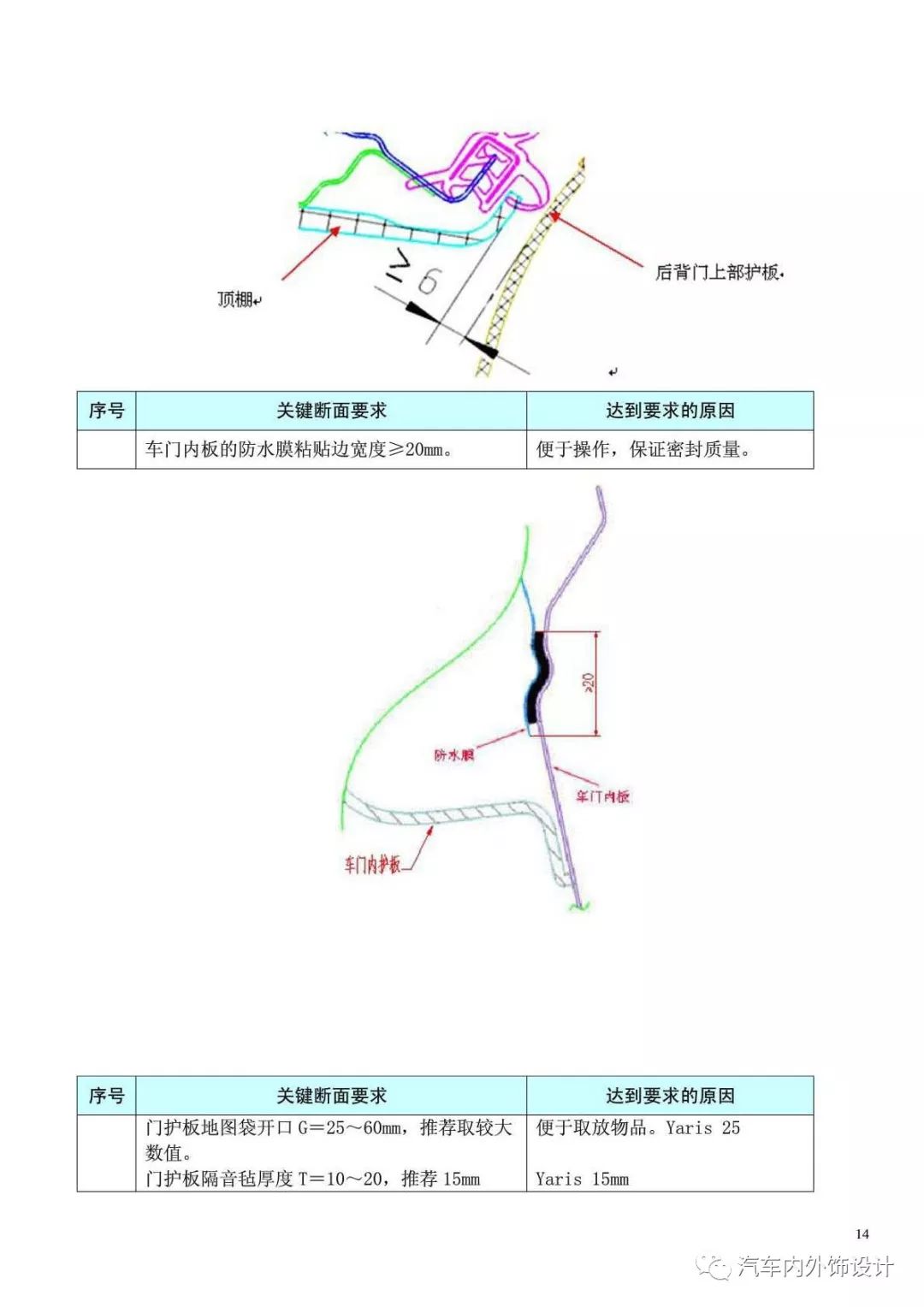
仪表板断面 干货 内外饰仪表板安装断面设计规范 怡姐话人物的博客 Csdn博客

覆工板 スチールデッキ（覆工板）の主材は、フランジ上面に格子模様のすべり止めを熱間圧延した縞h形綱です。これを一定寸法に切断して5本敷並 べ各要所を溶接により一体化し、側面を平板で補剛した、長方形板状をしています。 縞h 形鋼断面諸元標準断面 プレキャスト基礎板 地盤が良質でかつ、現場条件などにより急速施工が必要な場合は、プレキャスト基礎板にて据付が行えます。 標準据付歩掛はこちら 角材や厚い板で枠組みを作って、その裏と表にベニヤ板などの合板を貼った板 ということなんですね。 なので、こうやって断面図を見ると「中身がない」ってことになるわけです。 そんなわけで、このフラッシュ構造の板は叩くと

排水板 山东路易达新材料有限公司

肋板重合断面图怎么画 万图壁纸网

標準断面寸法（mm） 断面積 （cm 2 ） 重心の位置 （cm） 断面二次モーメント （l）（cm 4 ） 断面二次半径 （i）（cm） 断面係数 （Z）（cm 3 ） 高さ×辺×厚さ (H) × (B) × (t) r1 r2 a Cx Cy lx ly ix iy Zx Zy;断面図形 A：断面積（cm 2 ） e：図心からの距離（cm） I：断面二次モーメント（cm 4 ） Z：断面係数（cm 3 ） → I/e i：断面二次半径（cm） → √（I/A） 正方形 A = a 2 e = a/2 I = a 4 /12 Z = a 3 /6 i = a / √12 = 0267a 正方形 A = a 2 e = a / √2 I = a 4 /12 Z = a 3長方形断面 の曲げモーメント（断面二次モーメント）は次式より導出できる。 5 6 円形断面のねじりモーメントは断面二次極モーメントに等しいので次式より導出できる。 長方形断面の曲げ形状係数は基本形状を一辺b 0の矩形形状とすると、断面積に関して

创鑫激光 Maxphotonics Co Ltd

四板五带式道路断面图 图片欣赏中心 急不急图文 Jpjww Com

激光切割机加工厚板的常见问题

Fe3w楼承板 昆山市鑫中鑫彩钢制作安装工程有限公司

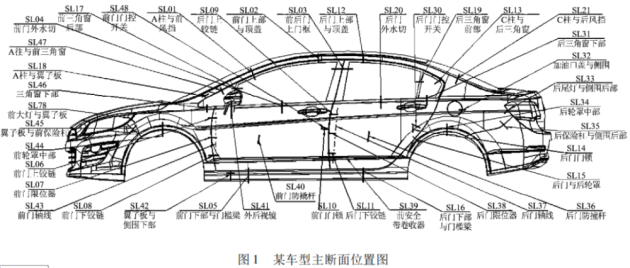
汽车白车身主断面控制要点 易车

钢筋混凝土过梁图集l11g303板桩断面图 钢筋切断机

斜管 斜板 产品

Mxb3525大断面铣齿机 液压拼板机厂家 自动拼板机 木结构集成材设备 木屋设备生产批发 烟台黄海木工机械有限公司

一块板道路横断面图 图片欣赏中心 急不急图文 Jpjww Com

排水板广泛用于屋顶花园 沼气池黑膜 厂家直销 接受定制

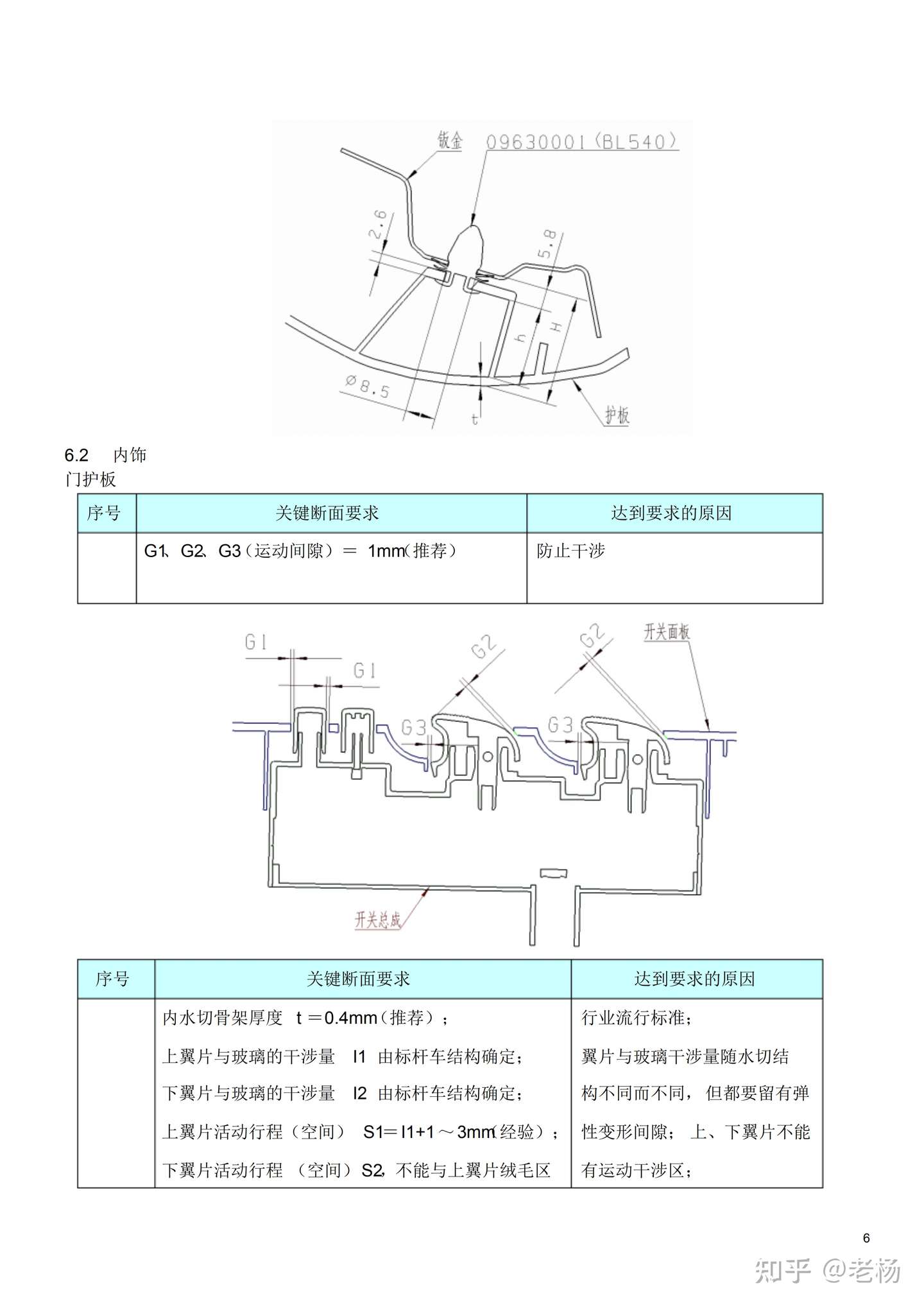
汽车内外饰设计 仪表板安装断面设计 知乎

建筑识图 分分钟教你弄清断面图与剖面图 雪花新闻

彩板门窗

如何设计明渠量水堰板安装示意图及断面图

南昌拟新建改造3条道路涉及红角洲 瑶湖片区 江西 手机江西网

塑料排水板 山东佳诺工程材料有限公司

断面钢格栅板 新型钢格栅板 镀锌网格板 江苏钢格栅板 价格厂家批发型号 富金机网

小径级原木制备大断面集成材技术与装备 等成果通过鉴定 中国人造板技术装备网

车身环状框架结构断面正向轻量化设计 乘用车轻量化 汽车轻量化在线 手机版

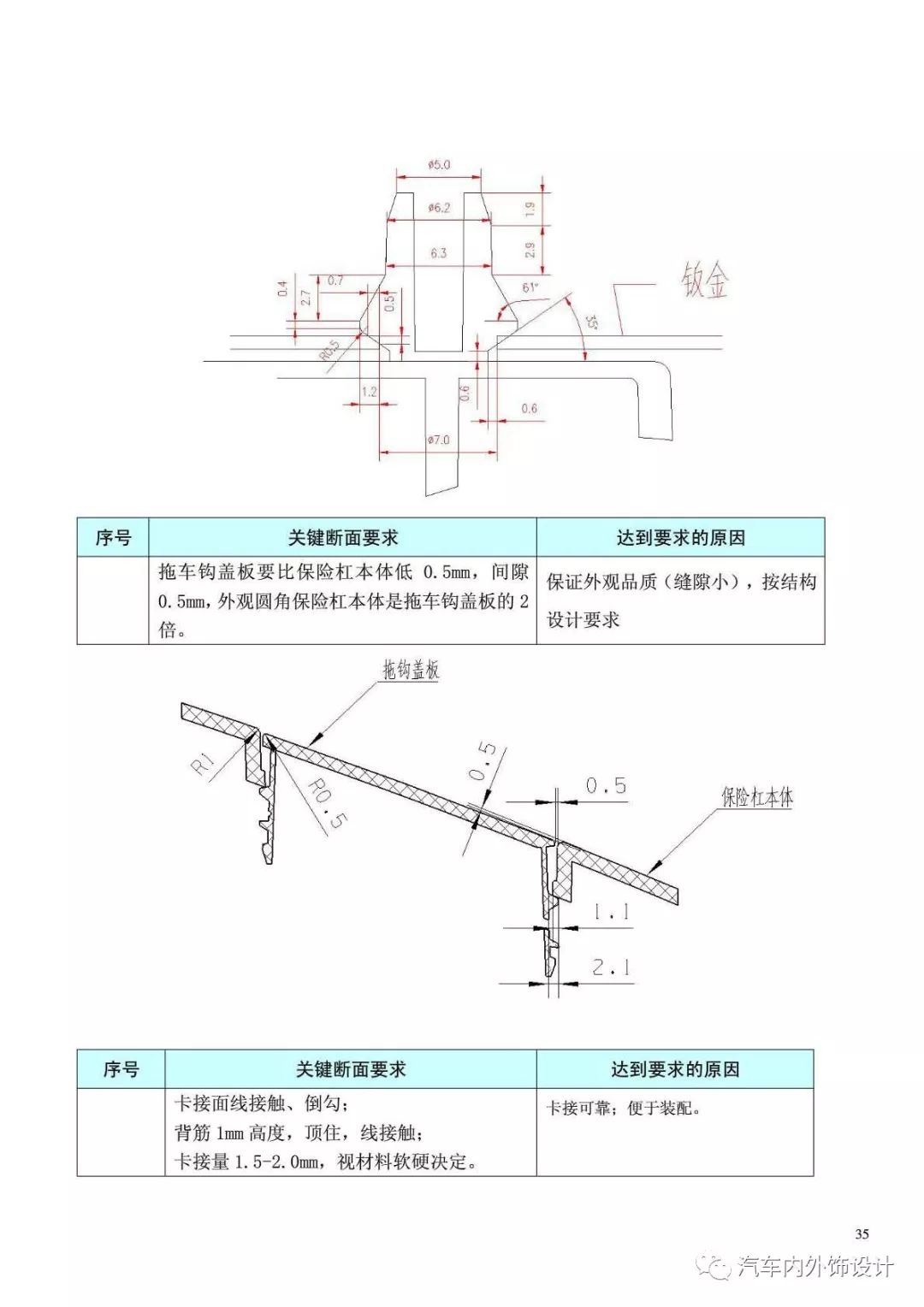
仪表板断面 干货 内外饰仪表板安装断面设计规范 怡姐话人物的博客 Csdn博客

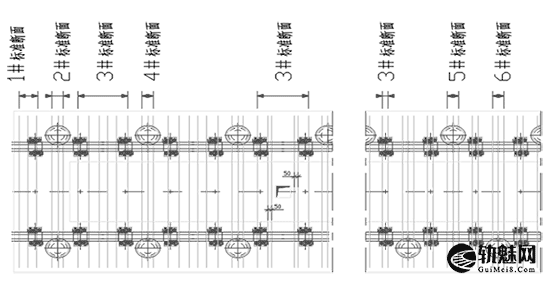
城市轨道交通现浇钢弹簧浮置板道床 钢筋笼轨排法 施工工艺

两块板道路断面 万图壁纸网

汽车内饰之 内饰之杂物箱区域仪表板断面 启飞专业知识系统分享 内饰断面07 启飞汽车设计培训

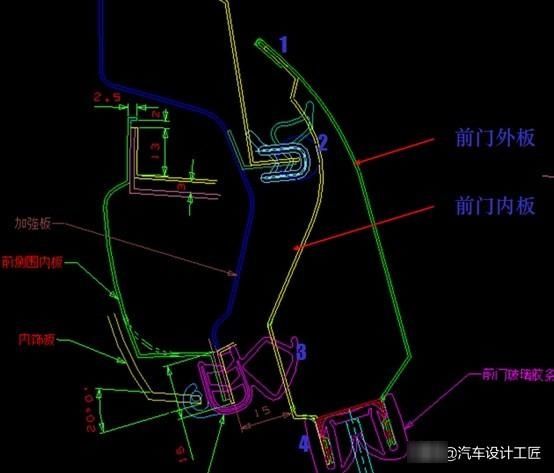
什么是汽车结构设计的前提 车身断面关键环节 这几个很重要 快资讯

Pc 聚碳酸酯 阳光板 这些断面你分得清嘛 上海绿澳新材料科技有限公司

泰山石膏板 宁波江北龙韵建材

汽车内饰之 门护板的四种经典断面 启飞专业知识系统分享 整车内饰开发37 启飞汽车设计培训

冰火板 山东兴华装饰材料有限公司

预计7月底通车 云卿路断头路即将打通 公交网

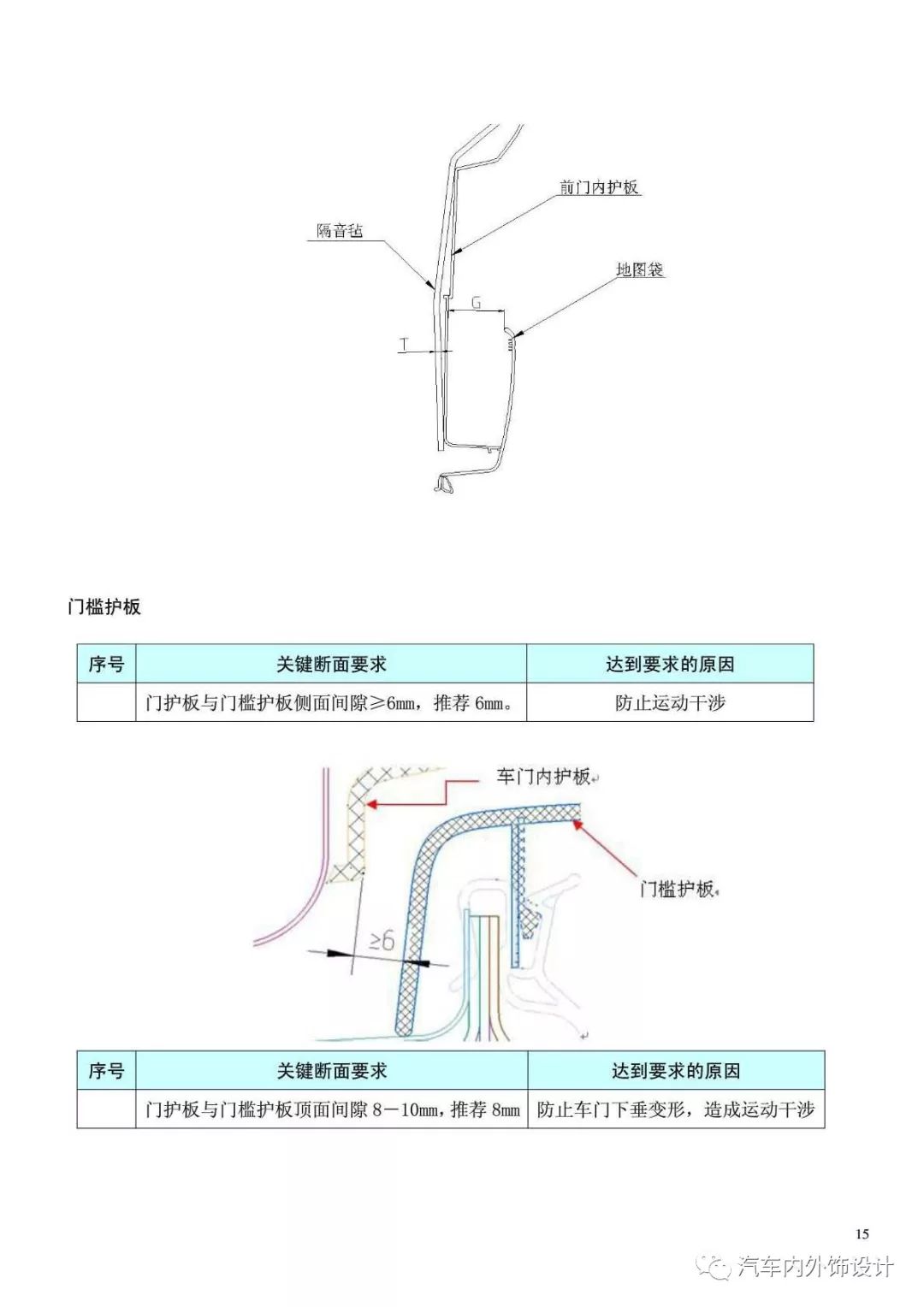
仪表板断面 干货 内外饰仪表板安装断面设计规范 怡姐话人物的博客 Csdn博客

加工板紹介 東京都森林組合

岩棉夹芯墙板 北京海强金诺国际轻钢板材有限公司

混凝土波形护栏板中走通信 供电管线的问题该如何解决 波形护栏板 防撞护栏 波形栏杆 贵州渝湘交通设施有限公司

背板断面図 段欠き 作っちゃう

汽车内饰之 内饰之通风盖板 顶盖 机盖断面 启飞专业知识系统分享 内饰断面03 启飞汽车设计培训

25 1讲什么是断面图 哔哩哔哩 つロ干杯 Bilibili

板梁 快懂百科

油泥模型 鼠标油泥模型制作过程一卡板断面做大型 哔哩哔哩 Bilibili

H型钢的横断面通常包括腹板和翼缘板两部分 行业资讯 山东巨海管业有限公司

如何设计明渠量水堰板安装示意图及断面图

产品分类 无锡日野换热设备有限公司

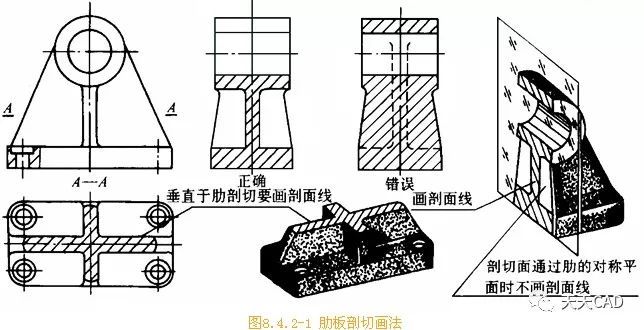
肋板画法

隔热采光板 屋面系统 产品中心 江苏林凯新材料有限公司

首钢京唐成功实现1800毫米板坯大断面 飞包 作业 生产

排水板 山东路易达新材料有限公司

路基沉降板观测断面及点的设置 元件布设 河北龙坤管道设备有限公司

红砂砖单色

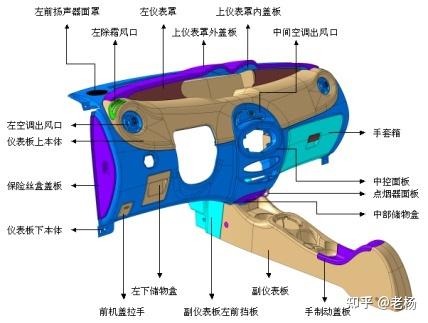
Catia怎样画内外饰断面 Catia断面图怎么画 Catia截取断面

排水板 山东金远方土工材料有限公司

排水板 山东金远方土工材料有限公司

一组常用道路断面图图一 信息图文欣赏 信息村 K0w0m Com

道路断面的基本形式 一块板 两块板 三块板

Diyの仕上げに便利 木口テープを使って木材の断面を飾ってみよう Limia リミア

常用板型断面图形

断面cad设计 新人首单立减十元 21年9月 淘宝海外

两块板道路断面 万图壁纸网

干货分享 光纤激光金属切割工艺改进的途径 光斑

道路断面形式示意图 信息评鉴中心 酷米资讯 Kumizx Com

另一种肌理的建筑外墙 压型金属板

道路断面形式示意图 信息评鉴中心 酷米资讯 Kumizx Com

轻质空心隔墙板 装配式建筑得分必备产品

黑龙江发明网

陕西博安机械工程有限公司

钢筋混凝土板断面图 搜狗图片搜索

汽车内外饰断面设计指南 每日头条

轻质隔音复合墙板

欧州足場板で代用検討ください 蕎麦アレルギーの木まぐれ日記 楽天ブログ

四板五带式道路断面图 图片欣赏中心 急不急图文 Jpjww Com

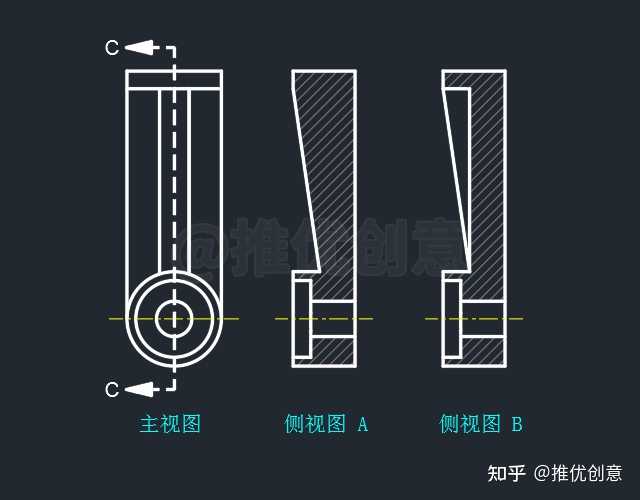
肋板重合断面图怎么画 十字肋板的重合断面图 肋板的断面图怎么画

汽车内外饰断面设计指南 每日头条

铝胎面板 5 Bar Metal Supplies Manbetx平台万博manbetx合法嘛 新万博官网注册 Manbetx平台 Manbetx客户端2 0客网

建筑工业化的起点 预制钢筋混凝土楼梯 现代建筑产业网

仓储货架 盒子板设备 99真人平台官网官方网站 中文版 超越平凡生活

分析如何处理鲁灰火烧板的断面 现象 哪家好 好的 电话 营销 山东泗水山岭石材厂 沈阳 哈尔滨 河南 湖北 河北 浙江 江苏 安徽 湖南 江西 陕西 内蒙古 常州 青岛 山东 菏泽 辽宁 吉林 济宁 临沂 云南 四川 广东

如何设计明渠量水堰板安装示意图及断面图

汽车内饰之 内饰之前风窗区域仪表板断面 启飞专业知识系统分享 内饰断面04 启飞汽车设计培训

剪板机剪切出平整断面的技巧 浙江华阳剪板机有限公司 技术支持

芦花板

Pc 聚碳酸酯 阳光板 这些断面你分得清嘛 上海绿澳新材料科技有限公司

Yxb35 125 750开口压型钢板技术参数 楼承板厂家 中国建筑用压型钢板全产业基地 上海新之杰官网

汽车内饰之 内饰之通风盖板 顶盖 机盖断面 启飞专业知识系统分享 内饰断面03 启飞汽车设计培训

榫卯36记 28 厚板出透榫拍抹头

车身主断面设计方法培训 光学社

车身环状框架结构断面正向轻量化设计 乘用车轻量化 汽车轻量化在线 手机版

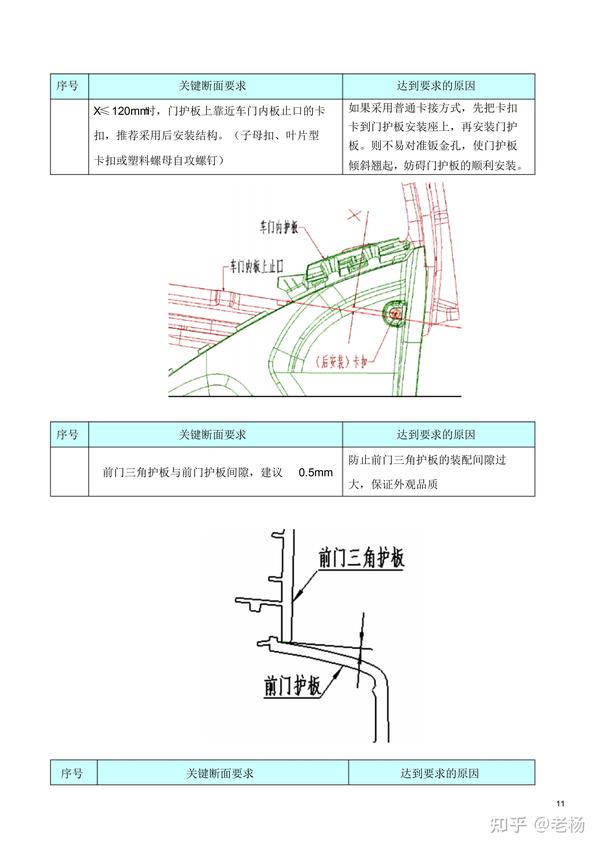
汽车内外饰设计 仪表板安装断面设计 知乎

钢波纹板结构在隧道工程中的应用 西安川交工程 以专业致匠心 建筑劳务分包建筑工程项目承包公路养护工程

板材知识早知道 板材十大品牌哪个更环保 企业新闻 板材 生态板 板材十大品牌 生态板十大品牌 广州佳力木业有限公司

河东东街延长线 港东路 港东二路 项目建设工程设计方案 手机网易网