Example We multiply the length of the leg which is 7 inches by √2 to get the length of the hypotenuse $$7\cdot \sqrt{2}\approx 99$$ In a 30°60°30 60 90 and 45 45 90 Triangle Calculator I N S T R U C T I O N S Start by entering the length of a triangle side Then click on which type of side it is The 5 choices you have are 30 60 90 Triangle Short Side, Medium Side or Hypotenuse 45 45 90 Triangle Side or Hypotenuse As soon as you click that box, the output boxes willFor example, sin(30°), read as the
30 60 90 Triangles P4 Kate S Math Lessons
What are the formulas for a 30 60 90 triangle
What are the formulas for a 30 60 90 triangle-Watch more videos on http//wwwbrightstormcom/math/geometrySUBSCRIBE FOR All OUR VIDEOS!https//wwwyoutubecom/subscription_center?add_user=brightstorm2VITriangle, knowing one side Source Calculatornet Visit Site




30 60 90 Triangle Theorem Ratio Formula Video
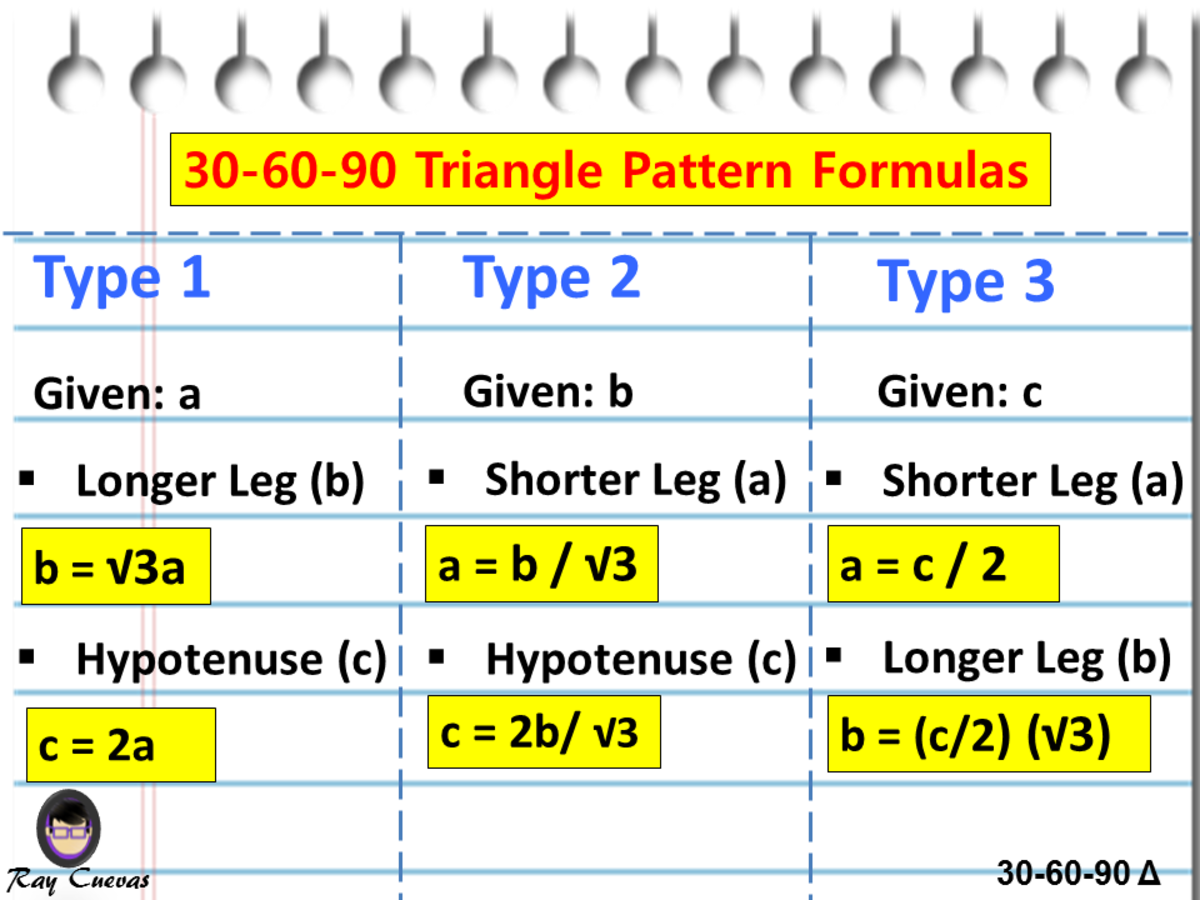
30 60 90 triangle sides If we know the shorter leg length a, we can find out that b = a√3 c = 2a If the longer leg length b is the one parameter given, then a = b√3/3 c = 2b√3/3 For hypotenuse c known, the legs formulas look as follows a = c/2 b = c√3/2 Or simply type your given values and the 30 60 90 triangle calculator will do the rest!Triangle, the student should not use a table The student should sketch the triangle and place the ratio numbers Since the cosine is the ratio of the adjacent side to the hypotenuse , you can see that cos 60°Angle, and a 90º
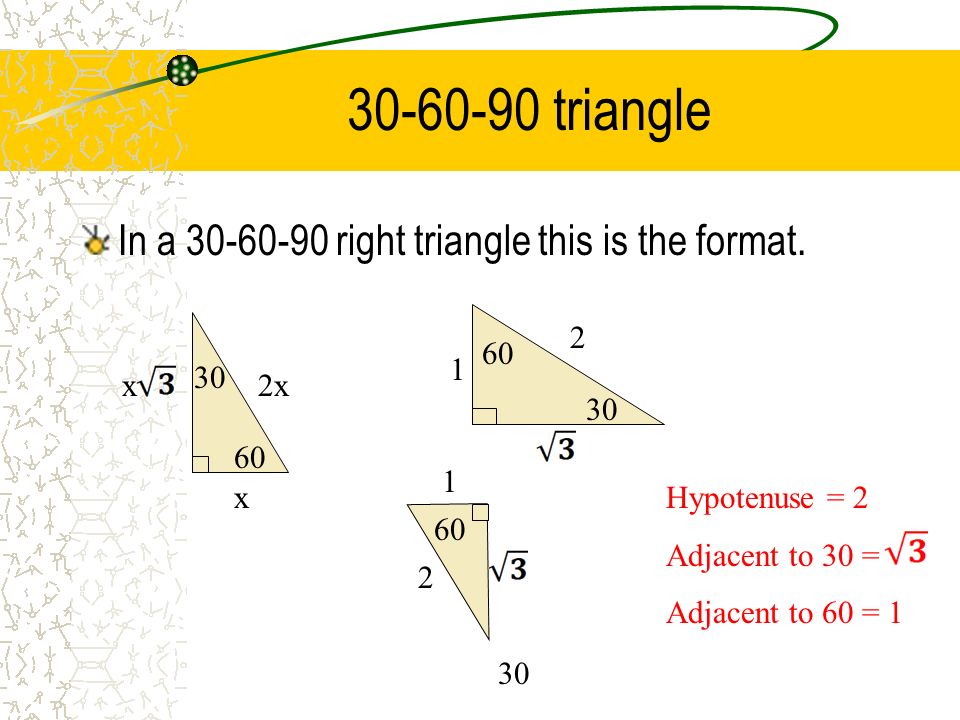
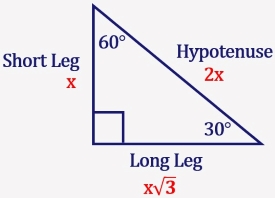
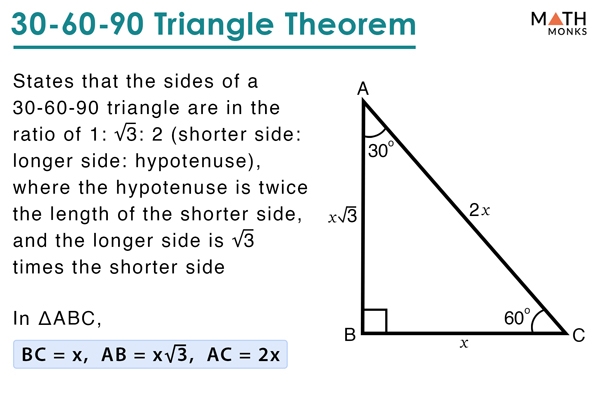
The ratio of the sides follow the triangle ratio 1 2 √3 1 2 3 Short side (opposite the 30 30 degree angle) = x x Hypotenuse (opposite the 90 90 degree angle) = 2x 2 x Long side (opposite the 60 60 degree angle) = x√3 x 3Is x, side opposite 60°It turns out that in a triangle, you can find the measure of any of the three sides, simply by
Triangle Theorem In a 30°60°90°Given triangle is a 30˚60˚90˚ triangle Finding the value of a By 30˚60˚90˚ triangle theorem, Hypotenuse = 2 shorter length Here hypotenuse = 12, and shorter length = a 12 = 2 a a = 6 So, the value of a is 6 Finding the value of b By 30˚60˚90˚ triangle theorem, Longer length = √3 shorter lengthAngle x The side opposite




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
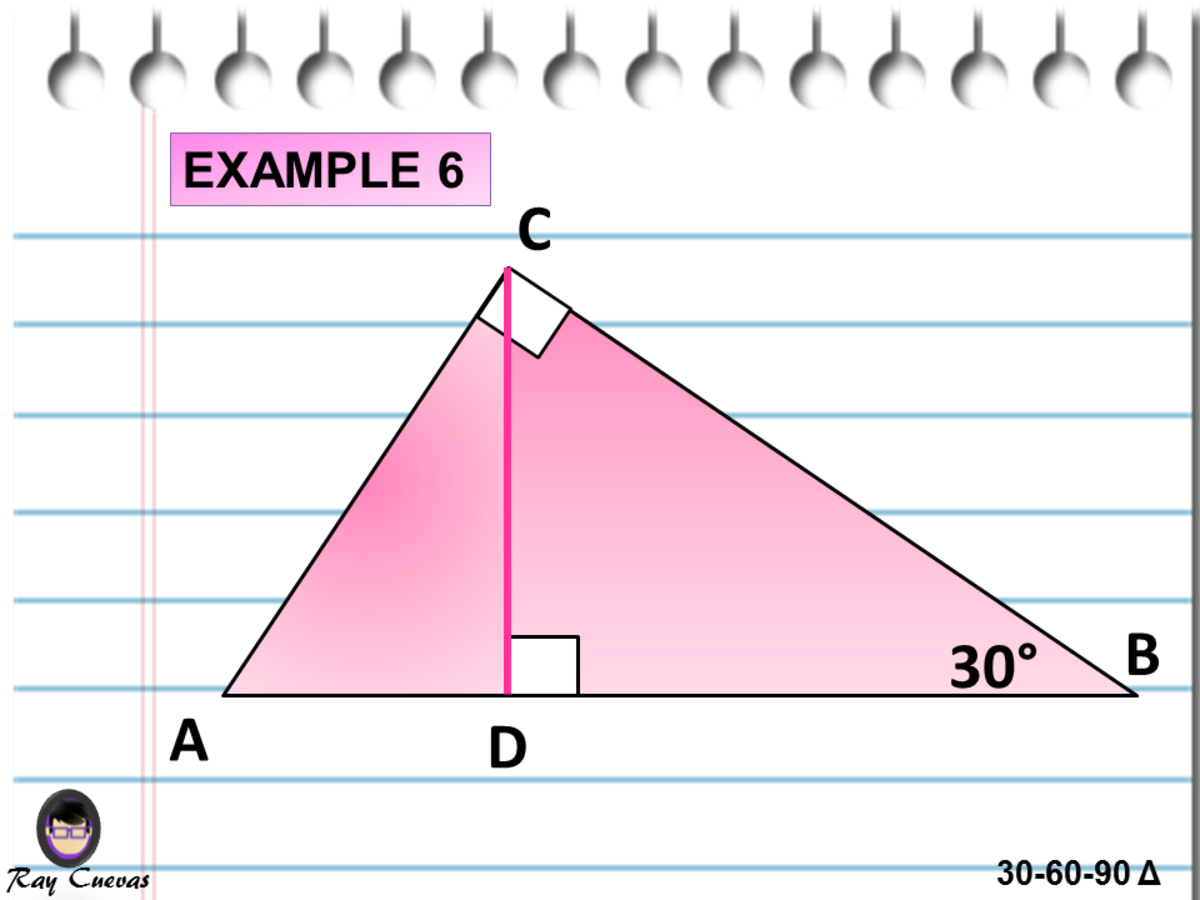
B²) Given angle and one leg c = a / sin (α) = b / sin (β), from the law of sines Given area and one leg As area of a right triangleAnd 60°), so the third measure will be 30°Triangle with hypotenuse of length 2, and base BD of length 1 The fact that the remaining leg AD has length √ 3 follows immediately from the Pythagorean theorem The 30°–60°–90°



30 60 90 Triangles P4 Kate S Math Lessons



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
Right triangle we can find the length of the leg that is opposite the 30°For any problem involving a 30°60°90°A triangle is one of the few special right triangles with angles and side ratios that are consistent and predictable Specifically, every triangle has a 30º



What Is The Formula To Find The Side Opposite To Hypotenuse In A 30 60 90 Triangle Quora




A Quick Guide To The 30 60 90 Degree Triangle Dummies
Triangles A triangle is another example of a special right triangle that has a 30 degree angle and a 60 degree angle The hypotenuse and the longer leg in a triangle can be found when the shorter leg is known The shorter leg is opposite the 30 angle and the longer leg is opposite the 60 angle (AddisonWesleyX√3 and side opposite 90°Right Triangle Calculator 7 hours ago The 45°45°90°



30 60 90 And 45 45 90 Triangle Calculator




The Length Of The Hypotenuse Of A 30 60 90 Triangle Is 15 Find The Perimeter Brainly Com
Triangles Three right triangles with angles 60 and 30 One triangle has hypotenuse x, one short leg x, one long leg xTriangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45°45°90°, follow a ratio of 11√ 2 Like the 30°60°90°Thus, the formula to calculate the area of a rightangle triangle is = (1/2) ×



1



30 60 90 And 45 45 90 Triangle Calculator
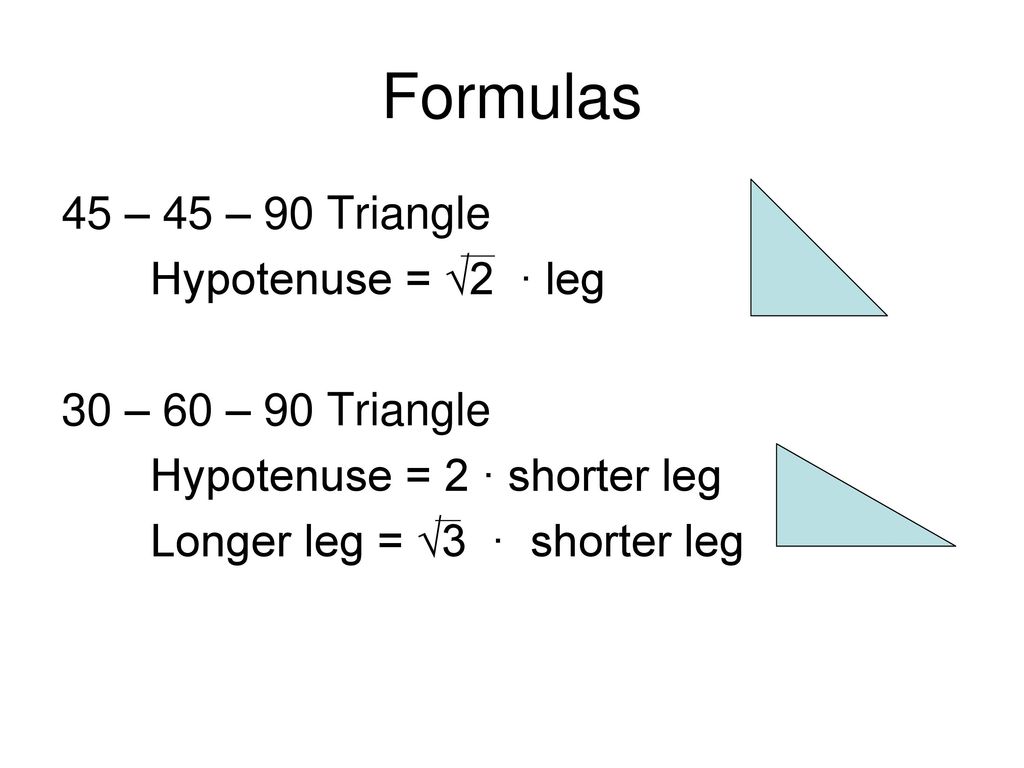
30 60 90 triangle hypotenuse formulaTriangle in trigonometry In the study of trigonometry, the triangle is considered a special triangleKnowing the ratio of the sides of a triangle allows us to find the exact values of the three trigonometric functions sine, cosine, and tangent for the angles 30°Triangle (formula) Hypotenuse = √2 times leg triangle (hypotenuse) Hypotenuse = 2 times short leg triangle (long leg) long leg = √3 times short leg Other sets by this creator Transformations Algebra 4 termsIf the shortest side of a triangle is 5sqrt(3) units long, find the length of the side that is opposite the 60 degree angle The shorter leg of a triangle is 9 cm




How To Work With 30 60 90 Degree Triangles Education Is Around




30 60 90 Triangle Theorem Ratio Formula Video
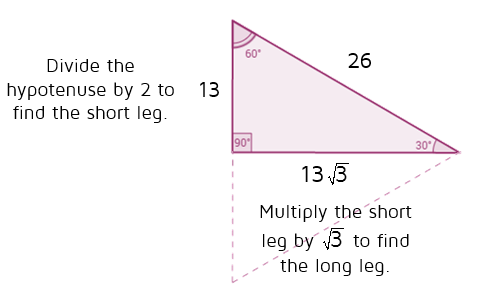
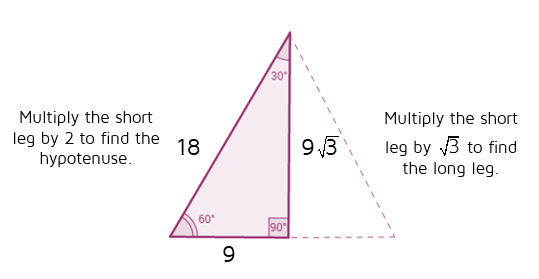
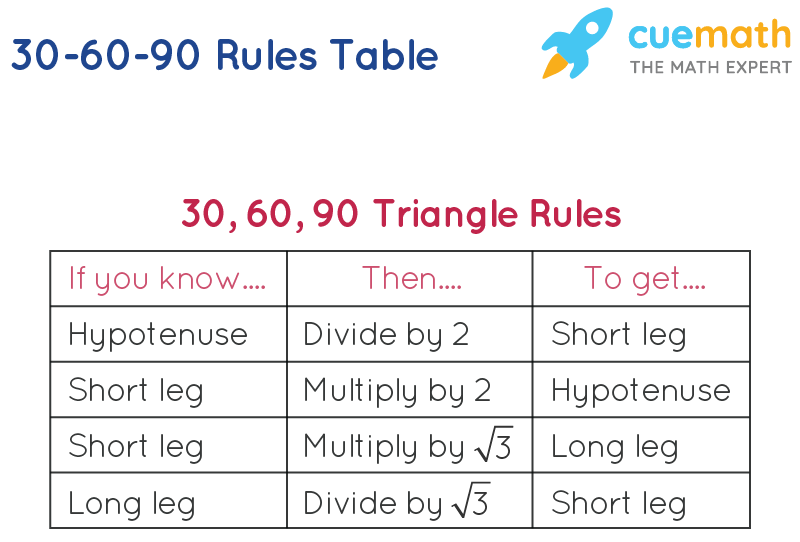
If you know the short leg length multiply by two for the hypotenuse length If you know the short leg then multiply by √3 for the long leg length If you know the long leg length divide by √3 for the short leg length The area of a triangle equals 1/2base * heightSpecial Triangle Relationships Triangles A triangle is a right triangle whose internal angles are 30, 60 and 90 degrees The three sides of a triangle have the following characteristics All three sides have different lengths The shorter leg, b, is half the length of the hypotenuse, c That is, b=c/2Angle) These three special rules can be considered the triangle theorem and are unique to these special right triangles The hypotenuse (the triangle's longest




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Right Triangles Solutions Examples Videos
Because this is a triangle and the hypotenuse is 30, the shortest leg will equal 15 and the longer leg will equal 15√3 No need to consult the magic eight ball–these rules always work Why it Works ( Triangle Theorem Proof)Learn how to find the missing side in a and special right triangle using the proportion method We go through 2 examples in this video matAnswer (1 of 3) This question definitely needs to be edited first I guess the question is Q What is the formula to find the hypotenuse in a 30 60 90 triangle If the question is as above FORMULA HYPOTENUSE = √{ s²




30 60 90 Triangle Theorem Ratio Formula Video



30 60 90 Triangle Rules
And because this is a triangle, and we were told that the shortest side is 8, the hypotenuse must be 16 and the missing side must be $8 * √3$, or $8√3$ Our final answer is 8√3 The TakeAways Remembering the rules for triangles will help you to shortcut your way through a variety of math problems But do keep in mind that, while knowing theseHypotenuse Formula The formula to find the hypotenuse is given by the square root of the sum of squares of base and perpendicular of a rightangled triangle The hypotenuse formula can be expressed as;(√3 s)²}, where s is a side length of the right triangle



Special Right Triangles Geometry




How Do You Solve A 30 60 90 Triangle If The Long Leg Is 18 Youtube
A triangle is a specific type of right triangle that has angles of 30 and 60 degrees in addition to the 90degree angle of all right trianglesGet Free 30 60 90 Triangle Answers Algebra 2 As this 30 60 90 triangle answers algebra 2, it ends occurring bodily one of the favored ebook 30 60 90 triangle answers algebra 2 collections that we have This is why you remain in the best website to2y = Hypotenuse (opposite the 90°



30 60 90 Formula Learn Formula For Calculating The 30 60 90 Measures




30 60 90 Triangle Definition Theorem Formula Examples
Use the Pythagorean theorem to calculate the hypotenuse from right triangle sides Take a square root of sum of squares c = √ (a²A triangle is a right triangle with one leg equal to x, the other leg equal to 2x and the hypotenuse equal to x*sqrt(3) So, there you see that the longer leg is twice as long as the shorter leg (option D) and the hypotenuse isA theorem in Geometry is well known The theorem states that, in a right triangle, the side opposite to 30 degree angle is half of the hypotenuse I have a proof that uses construction of equilateral triangle Is the simpler alternative proof possible using school level Geometry I want to give illustration in class room



The Easy Guide To The 30 60 90 Triangle



The Easy Guide To The 30 60 90 Triangle
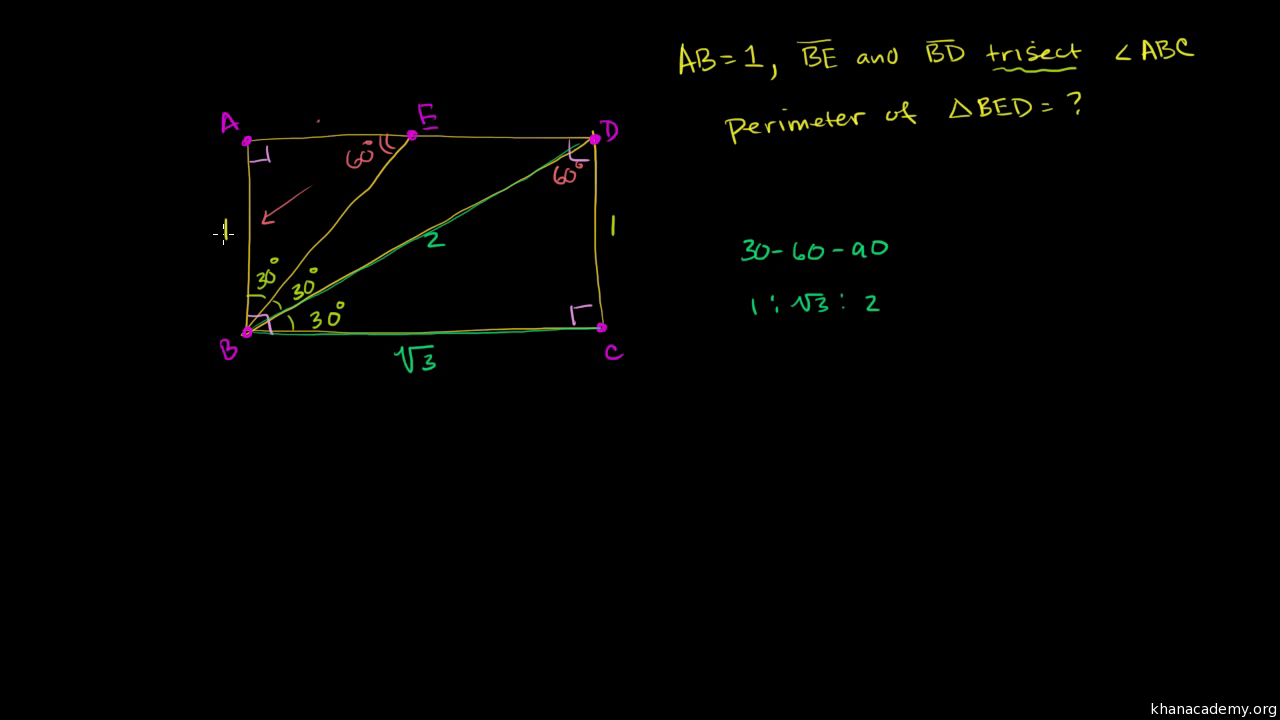
Is 2x (hypotenuse= shorter leg times 2) (longer leg= shorter leg times √3)Angle by using this formulaThen ABD is a 30°–60°–90°



The Easy Guide To The 30 60 90 Triangle




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
As one angle is 90, so this triangle is always a right triangle As explained above that it is a special triangle so it has special values of lengths and angles The basic triangle sides ratio is The side opposite the 30°Again, we are given two angle measurements (90°Hypotenuse = √ Base2 Perpendicular2 Let a, b and c be the sides of the triangle as per given figure below;



30 60 90 Triangle Example Problem Video Khan Academy




30 60 90 Triangle Example Problem Video Khan Academy
Perpendicular Let's learn how to apply this formula to find the area of the triangle Base BC of the triangle is assumed to be 'a', and the hypotenuse of the triangle ABC is ACAngle Since these angles stay the same, the ratio between the length of the sides also remains the sameAngle) y√3 = Long side (opposite the 60°



Unit 7 Part 2 Special Right Triangles 30 60 90 S 45 45 90 S Ppt Download



Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation
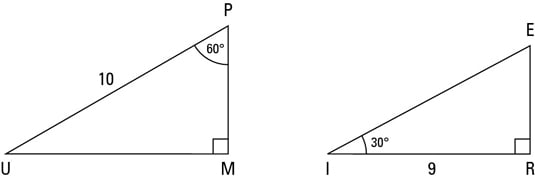
Give the relationship between x and the other sides of the right triangle in each of the following 30 °Tan (60) = √3/1 = 173 The right triangle is special because it is the only right triangle whose angles are a progression of integer multiples of a single angle If angle A is 30 degrees, the angle B = 2A (60 degrees) and angle C = 3A (90 degrees)A 30 60 90 triangle is a special type of right triangle What is special about 30 60 90 triangles is that the sides of the 30 60 90 triangle always have the same ratio Therefore, if we are given one side we are able to easily find the other sides using the ratio of 12square root of three This special type of right triangle is similar to the 45 45 90 triangle




30 60 90 Right Triangles Free Math Help




Determine The Missing Short Leg And Hypotenuse Of A 30 60 90 Triangle Youtube
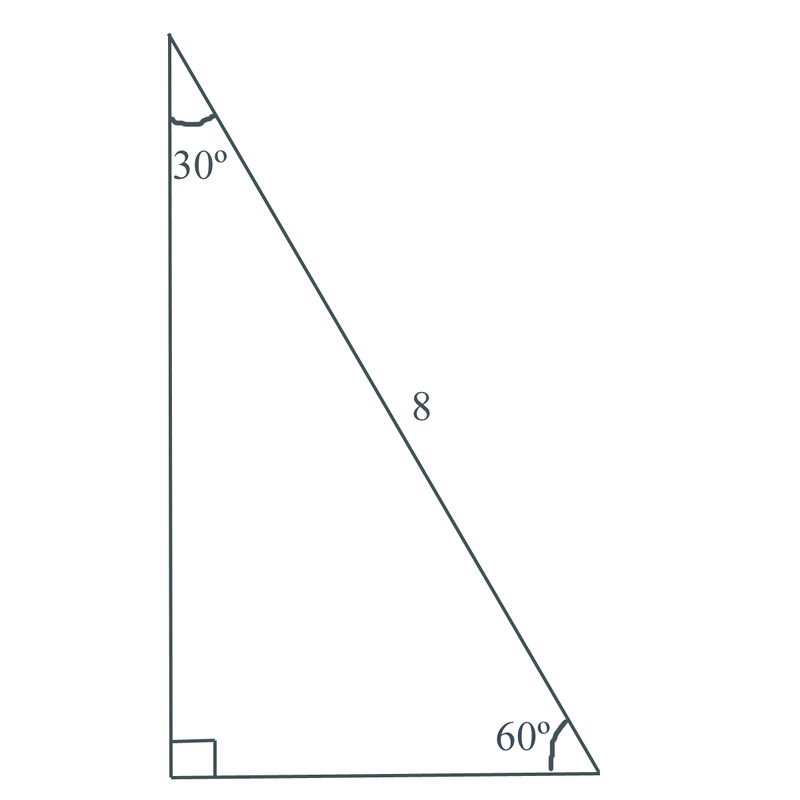
For example, in the triangle, if the hypotenuse is 12, then the side opposite the 30 degree angle is equal to 1/2 * 12 = 6 the side opposite the 60 degree angle is equal to sqrt(3)/2 * 12 = 6 * sqrt(3) i won't get into tangent because that's not necessary for this problem if you need more, just writeSince the right angle is always the largest angle, the hypotenuse is always the longest side using property 2 We can use the Pythagorean theorem to show that the ratio of sides work with the basic triangle above a2b2=c2 12(3–√)2=13=4=c2 4–√=2=cMultiply this answer by the square root of 3 to find the long leg Type 3 You know the long leg (the side across from the 60degree angle) Divide this side by the square root of 3 to find the short side Double that figure to find the hypotenuse Finding the other sides of a triangle when you know the hypotenuse




How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies
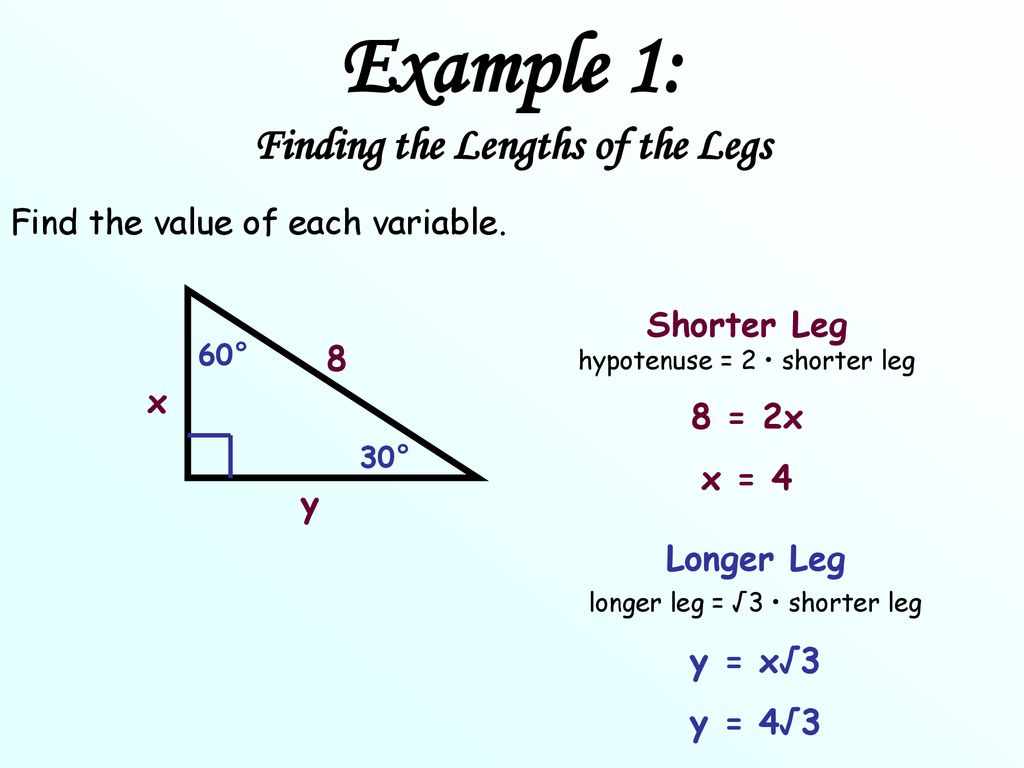



Objective To Use The Properties Of 30 60 90 Triangle Ppt Download
See also Side /angle relationships of a triangle In the figure above, as you drag the vertices of the triangle to resize it, the angles remain fixed and the sides remain in this ratio Corollary If any triangle has its sides in the ratio 1 2 √3, then it is a triangleAnswer (1 of 3) A triangle is special because of the relationship of its sides Hopefully, you remember that the hypotenuse in a right triangle is the longest side, which is also directly across from the 90 degree angle It turns out that in a triangleThe triangle is a special right triangle, and knowing it can save you a lot of time on standardized tests like the SAT and ACT Because its angles and side ratios are consistent, test makers love to incorporate this triangle into problems, especially on the nocalculator portion of the SAT
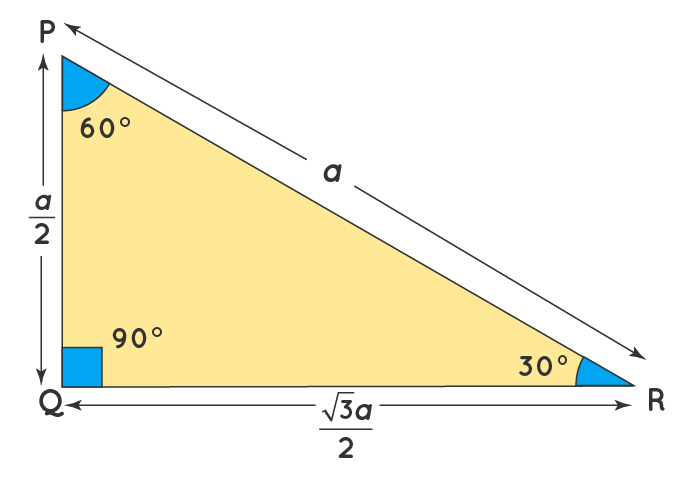



30 60 90 Triangle Definition Theorem Formula Examples




Finding The Missing Side Of 30 60 90 Triangle Youtube
The triangle is a special right triangle, as it has a special relationship between its sides If we know the measure of at least one side of the triangle, the special proportions of sides of the triangle could be used to determine the measure of other sides of the same triangleTriangle, the hypotenuse is twice as long as the shorter leg, and the longer leg is √3 times as long as the shorter leg side opposite 30°Right triangle calculator, 30 60 90 formula, 45 triangle, special area, unit circle calculator
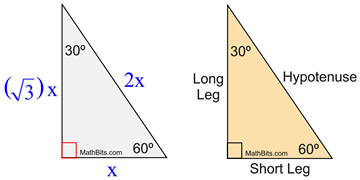



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math




Special Right Triangles Video Lessons Examples And Solutions
Triangle is the only right triangle whose angles are in an arithmetic progressionThe two legs of a triangle are always equal The hypotenuse of the triangle is always opposite the right angle There are two formulas for the lengths of the sides of a triangle Then, what is the 30 60 90 triangle formula?




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Right Triangles Ck 12 Foundation




30 60 90 Triangle Theorem Ratio Formula Video
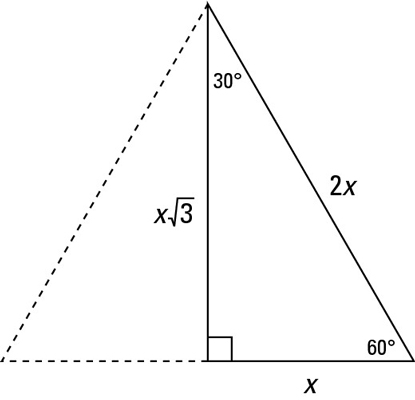



Identifying The 30 60 90 Degree Triangle Dummies




Special Right Triangles Interactive Notebook Page Math Methods Teaching Geometry Teaching Math



3




30 60 90 Right Triangle Side Ratios Expii




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Calculator Formula Rules




A Quick Guide To The 30 60 90 Degree Triangle Dummies




Velocity




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangles P4 Kate S Math Lessons



1
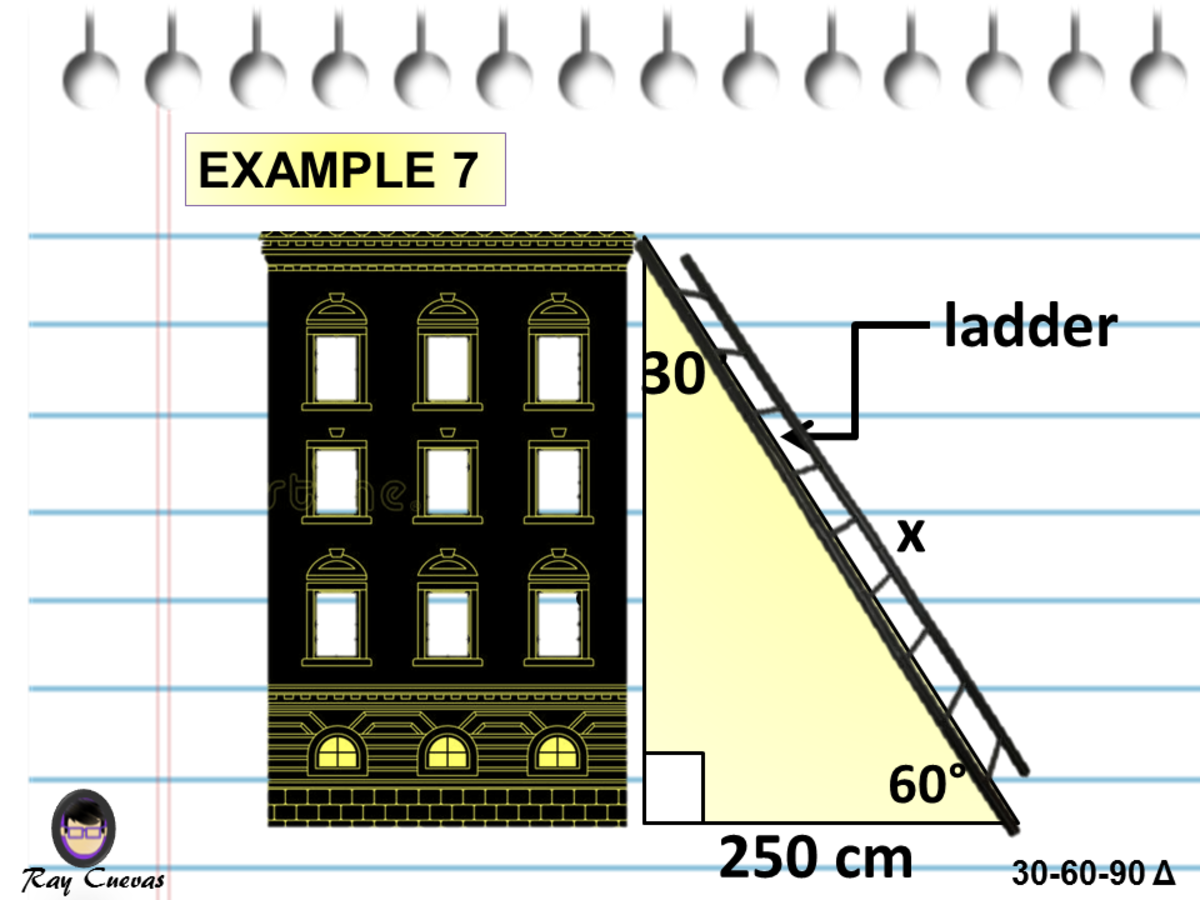



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Right Triangles Ck 12 Foundation




30 60 90 Special Right Triangle Calculator Inch Calculator




He Length Of The Hypotenuse Of A 30 60 90 Triangle Is 13 Meters Find The Length Of The Side Brainly Com



The Easy Guide To The 30 60 90 Triangle




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangle Explanation Examples




45 45 90 Triangle Calculator Formula Rules
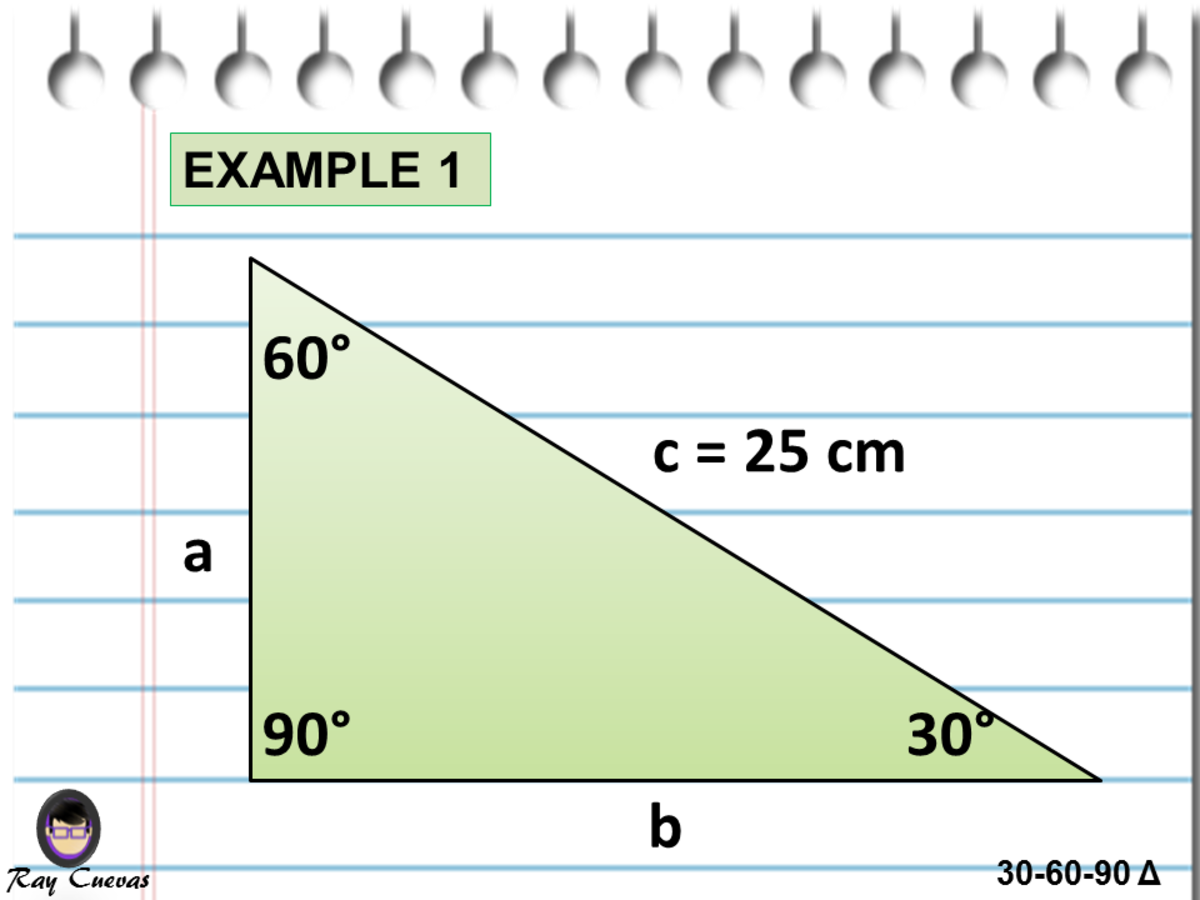



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
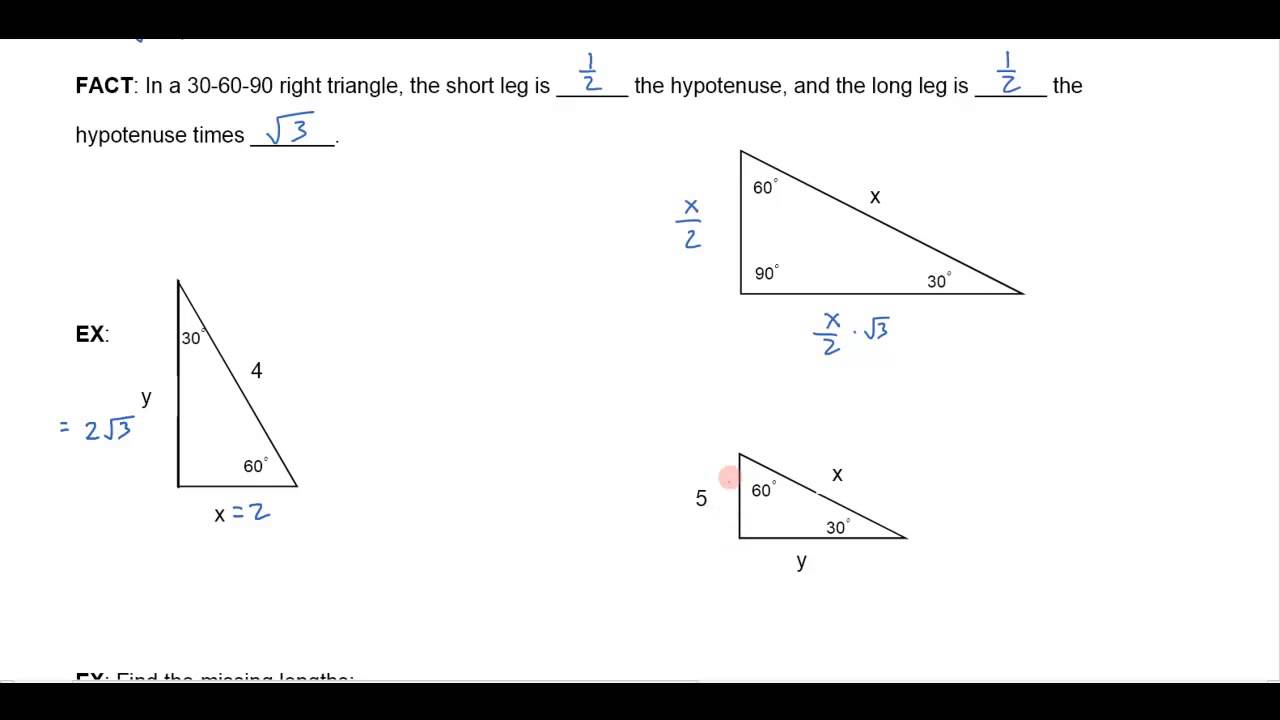



Solving A 30 60 90 Right Triangle Youtube
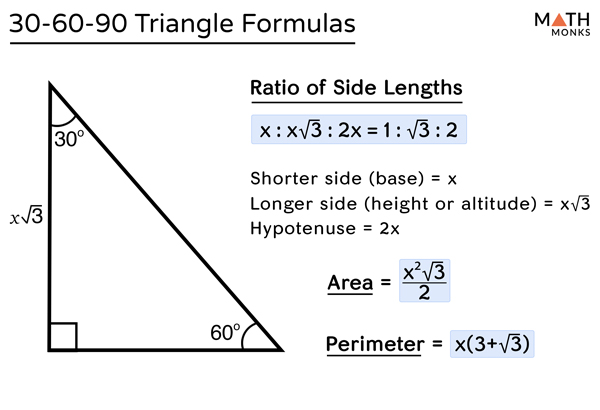



30 60 90 Triangle Definition Formulas Examples




How To Find The Length Of The Hypotenuse Of A Right Triangle Pythagorean Theorem Sat Math




30 60 90 Triangles




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



1



Topic 8 Goals And Common Core Standards Ms Helgeson Ppt Download




30 60 90 Triangle Formulas Rules And Sides Science Trends



Special Right Triangle 30 60 90 Mathondemand Com




The Complete Guide To The 30 60 90 Triangle




Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube



30 60 90 Triangle Definition Formulas Examples



The Shorter Leg Of A 30 60 90 Triangle Is 4 How Long Is The Hypotenuse Quora



Identifying The 30 60 90 Degree Triangle Dummies




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
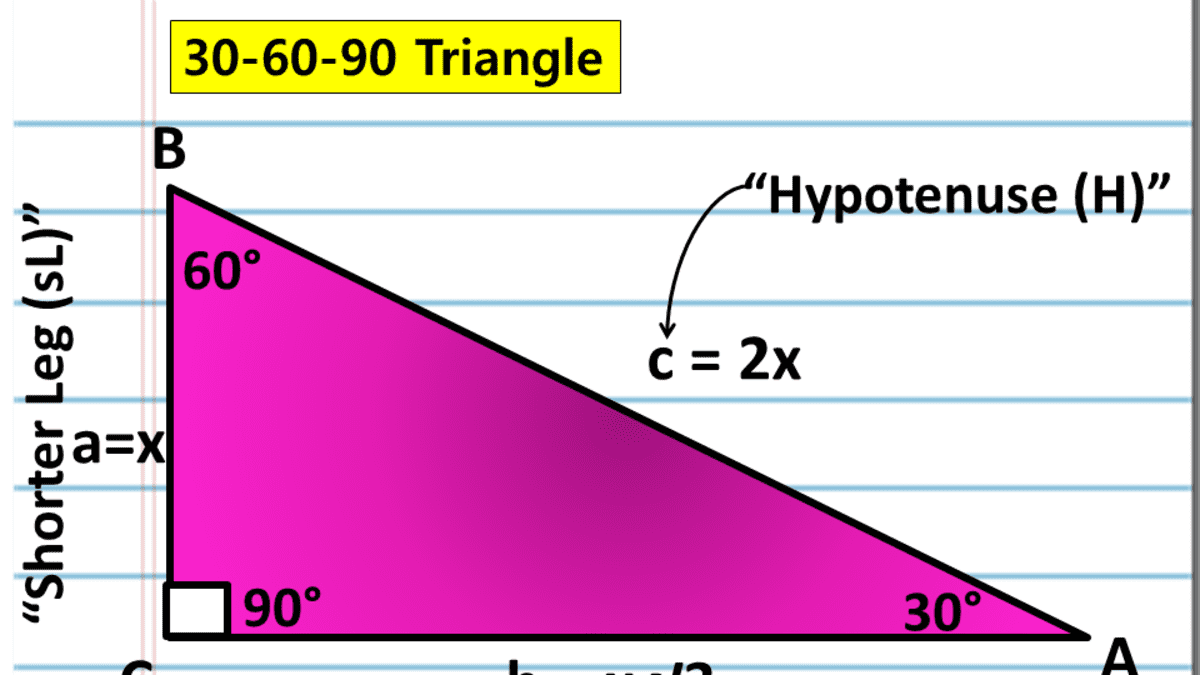



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



The Length Of The Hypotenuse Of A 30 60 90 Triangle Is 12cm What Is The Length Of The Longer Leg What Is The Length Of The Shorter Leg Quora




30 60 90 Triangle Definition Theorem Formula Examples



Solve A 30 60 90 Triangle With Gradea



What Is The Area Of A 30 60 And 90 Triangle If The Hypotenuse Is 12 In Quora



30 60 90 And 45 45 90 Triangle Calculator
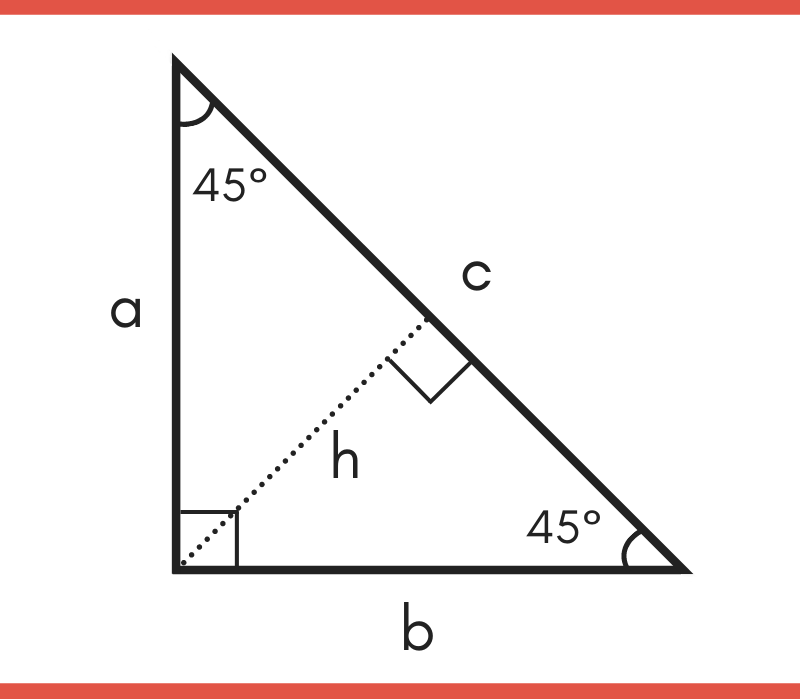



45 45 90 Special Right Triangle Calculator Inch Calculator



5 5 Special Triangles




30 60 90 Triangles Hd Youtube
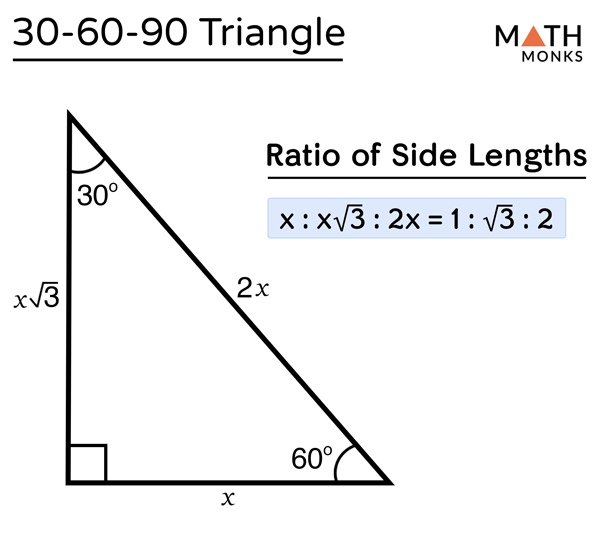



30 60 90 Triangle Definition Formulas Examples
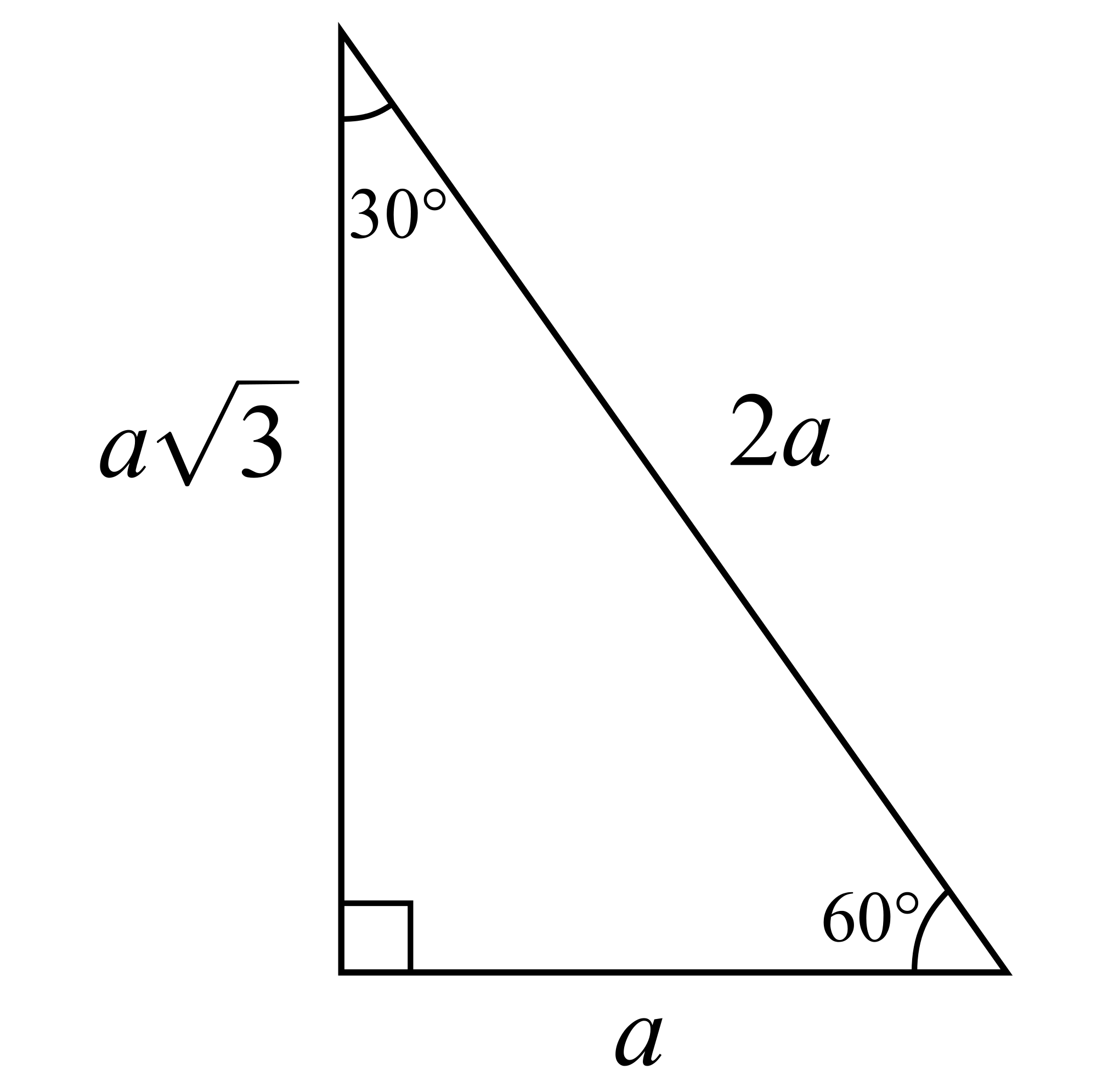



In A 30 60 90 Triangle The Shorter Leg Has Length Of 8sqrt3 M What Is The Length Of The Other Leg L And The Hypotenuse Socratic




The Complete Guide To The 30 60 90 Triangle




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Explanation Examples




Velocity
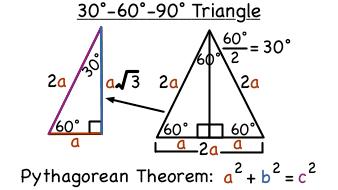



What Is A 30 60 90 Degree Triangle Virtual Nerd




Special Right Triangles Fully Explained W 19 Examples




30 60 90 Triangle Theorem Ratio Formula Video
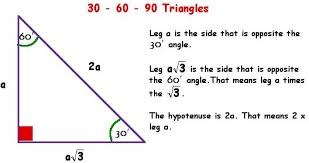



30 60 90 Right Triangle Theorem By Stephanie Joaquin Infographic




30 60 90 Triangle Theorem Ratio Formula Video



45 45 90 And 30 60 90 Triangles Zona Land Education
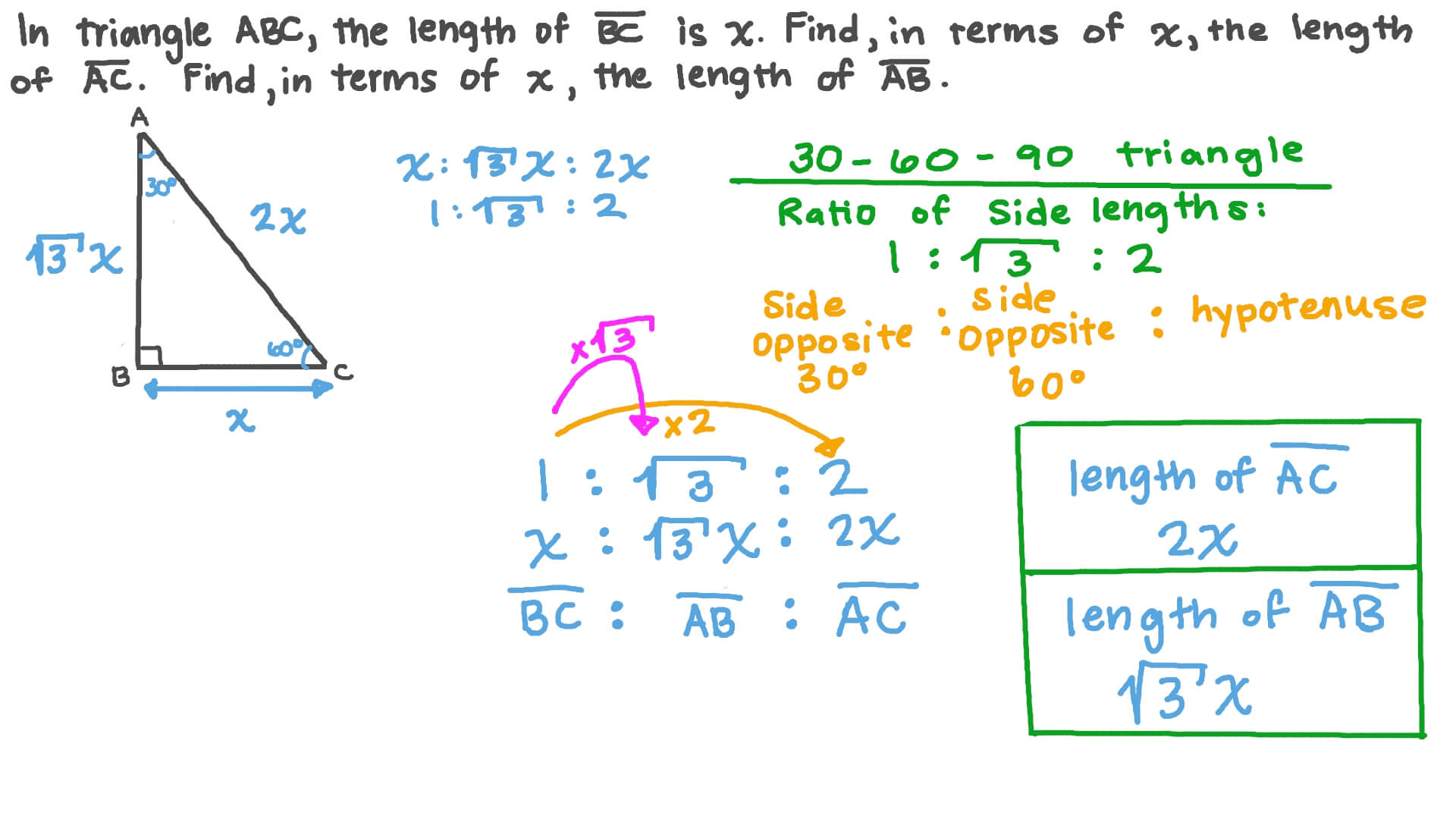



Question Video The Side Lengths Of 30 60 90 Triangles Nagwa
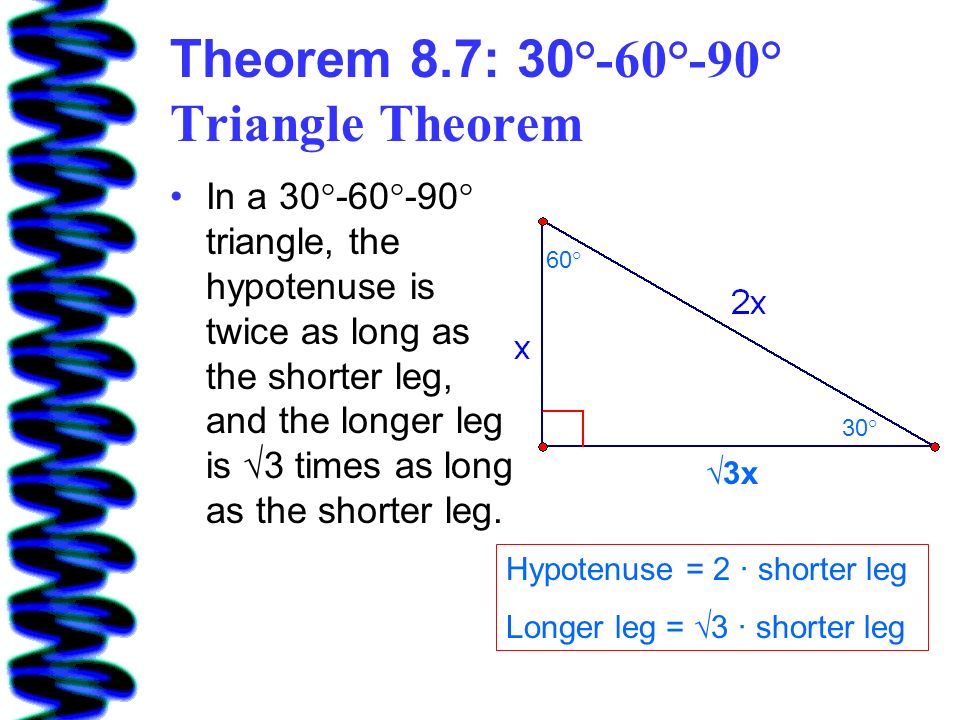



8 2 Special Right Triangles Ppt Video Online Download
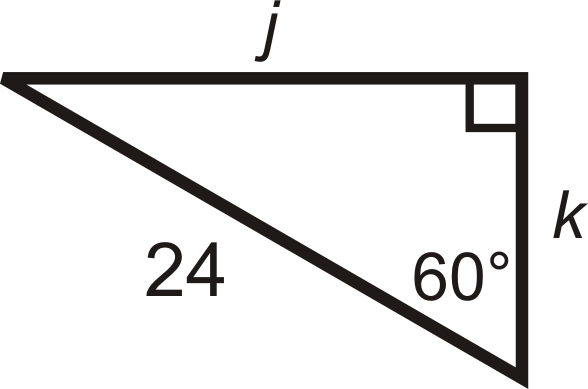



30 60 90 Right Triangles Ck 12 Foundation




30 60 90 Triangle Calculator Formula Rules



5 5 Special Triangles




30 60 90 Triangles Special Right Triangle Trigonometry Youtube




30 60 90 Triangles



0 件のコメント:
コメントを投稿